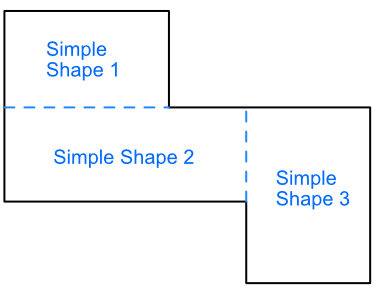
A compound shape is a shape that is built up from two or more simple shapes. A simple shape is a shape for which a formula for calculating area is readily available, such as triangles, rectangles and circles.
To calculate the area of a complex shape, divide the complex shape into a number of simple shapes. There are often a number of ways to divide the shape up: it does not matter which combination is used so long as the whole complex shape is taken into account.
The area of each simple shape is calculated separately; then added together as a total for the compound shape.
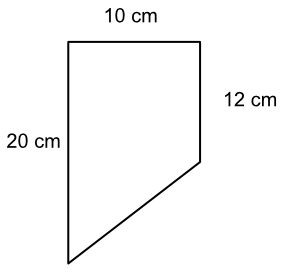
What is the area of this shape?
Split the compound shape into two simple shapes: a rectangle and a triangle:
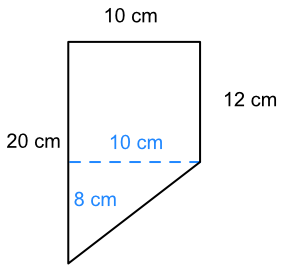
The area of the rectangle part is 12 x 10 = 120 cm2.
The missing dimension for the triangle part is 20 - 12 = 8cm.
| Area of a triangle | A | = `frac(1)(2)bh` |
| Substitute: | = `frac(1)(2) xx 10 xx 8` | |
| = 40 cm2. |
Area of compound shape
= area of rectangle + area of triangle
= 120 + 40
= 160 cm2.
Answer: 160 cm2
A stained glass window is being manufactured as the centrepiece of a new home. The stained glass will cost £250 per square metre. How much will the stained glass cost for the window?
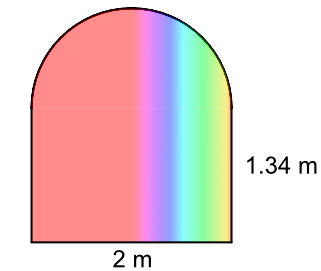
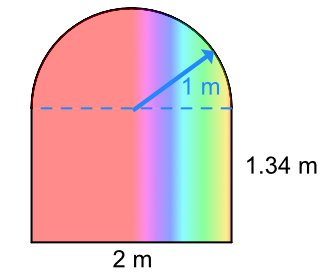
The lower part of the window is a rectangle:
| Area of a rectangle | A | = `b xx h` |
| Substitute: | = `2 x 1.34` | |
| = 2.68 cm2. |
The upper part of the window is a semicircle (half a circle).
The diameter of the semicircle is the width of the window;
the radius is half of that = 1m.
| Area of a whole circle | A | = `πr^2` |
| Area of a semicirclee | A | = `frac(1)(2) xx πr^2` |
| Substitute: | = `frac(1)(2) xx π xx 1^2` | |
| = 4.25 cm2. |
Area of entire window = 2.68 + 1.57 = 4.25 m2
Cost of window = 250 x 5.82 = £1062.50
Answer: £1062.50