Circle Theorems - Segment Angles

Given that the angle at the centre of a circle is twice the angle at the circumference when subtended by the same arc:

Angle ∠COD, below, is twice ∠CAD as it is subtended by the same arc. Similarly, ∠COD is twice the angle of ∠CBD. Therefore ∠CAD = ∠CBD.

Angles at the circumference are equal when subtended by the same arc.

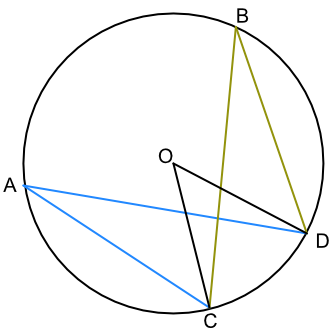
Circle theory: segment angles

Example 1

What is the value of the angle ∠BCD?

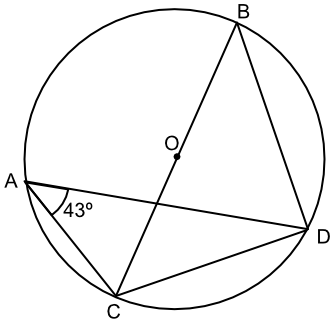
Circle theory: use segment angles to work out another angle

Angles in the same segment are equal: ∠CAD = ∠CBD = 43º

The angle in a semicircle is a right angle: ∠BDC = 90º

Angles in a triangle add to 180º: ∠BCD = 180 - 90 - 43 = 47º

Answer: 47º

What is the value of the angle ∠ADB?

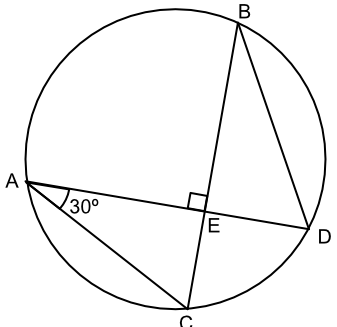
Circle theory: angles in the same segment are equal

Angles in the same segment are equal: ∠CAD = ∠CBD = 30º

Angle ∠DEB is a right angle = 90º

Angles in a triangle add to 180º: ∠BDE = 180 - 90 - 30 = 60º

∠BDE and ∠BDA are the same angle = 60º

Answer: 60º