A congruent triangle means that it is the same size as another triangle. However, the congruent triangle may be rotated or reflected, and may not look the same.
A similar triangle is a triangle that has the same angles, but has different lengths of sides. Note that each side of a similar triangle is in the same ratio as the corresponding side on the other triangle.
A corresponding triangle may be found by checking conditions of congruence. These are:
All three sides are equal (side-side-side, or SSS)
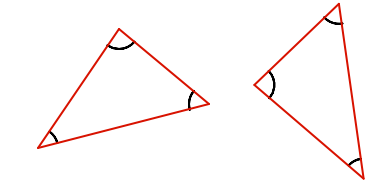
Two sides, and the included angle (between the two sides) are all equal (side-angle-side, or SAS)
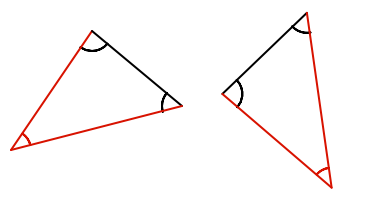
Two angles and a corresponding side - the same side on each triangle - are equal (angle-angle-side, or AAS)
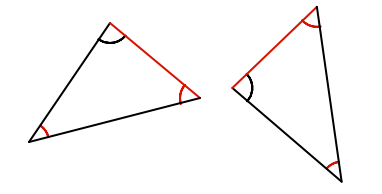
For a right-angled triangle, the hypotenuse and one other side are equal (right angle - hypotenuse - side, or RHS)
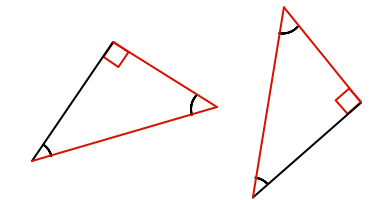
Are these two triangle congruent?

Checking using SAS (side - angle - side)
5cm-34º-7cm is not the same as 5cm-34º-8cm
Answer: No
Are all right-angles triangles with shorter sides of 3cm and 4cm congruent?
From Pythagoras, the hypotenuse on each of these triangles will be 5cm. Using RHS - it is a right angled triangle, the hypotenuse is 5cm and at least one of the other sides is the same length on each triangle.
Answer: Yes