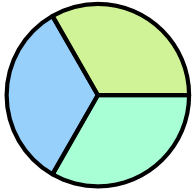
A fraction divides an item into smaller, equal, parts. Divide a circle into three equal parts: all three slices together will make a whole circle, but the circle itself has been divided by 3.
As a fraction, this is written as `frac(1)(3)`, which is another way of writing 1 ÷ 3. The top number is the numerator, and the bottom number is the denominator.
Two slices of the circle will be 2 x `frac(1)(3)`, and is written as `frac(2)(3)` (two lots of `frac(1)(3)`).
If each original slice is further divided in two, there will be six slices: each slice will be `frac(1)(6)` of the circle.
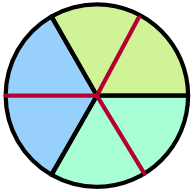
Two of the divided slices will be the same size as one of the original slices: `frac(2)(6)` = `frac(1)(3)`. This is an equivalent fraction: two fractions are equivalent if they have the same value, even if they are composed of different numbers.
Equivalent fractions can be obtained by multiplying or dividing the numerator and denominator by the same number:
`frac(1^(times2))(4_(times2)) = frac(2^(times2))(8_(times2)) = frac(4)(16)`
Dividing numerators and denominators by the same number will make them smaller. This is called simplifying. When the fraction cannot be simplified any more, it is in its simplest form.
`frac(6^(÷3))(12_(÷3)) = frac(2^(÷2))(4_(÷2)) = frac(1)(2)`
A common fraction, sometimes also called a vulgar fraction, is a fraction where both the numerator and the denominator are integers.
Put `frac(9)(27)` into its simplest form.
Divide both the numerator and denominator by 9.
`frac(9)(27) = frac(9^(÷9))(27_(÷9)) = frac(1)(3)`
It is also possible to divide top and bottom by 3, then to divide by 3 again, to get the same answer.
Answer: `frac(1)(3)`
Which of the following fractions are equivalent to `frac(3)(8)`?
`frac(1)(4)` , `frac(6)(16)` , `frac(8)(3)` , `frac(12)(32)` , `frac(3)(4)`
`frac(6)(16)` is `frac(3^(xx2))(8_(xx2))` and `frac(12)(32) = frac(3^(xx4))(8_(xx4))`
Answer: `frac(6)(16)` and `frac(12)(32)`
See also Terminating Decimals and Fractions