General Triangles

Pythagoras` Theorem and the Trigonometric ratios (sin, cos, tan) require right-angled triangles. Both the theorem and the trigonometric ratios can be used on more general triangles that do not contain a right angle.

Triangles can be divided into two smaller triangles:

Triangle divided into two right angled triangles

In this instance, the vertical height is the same for both smaller triangles. This vertical height can also be used to work out the area of the triangles.

If angles are given, the sin rule or the cosine rule are more likely to be used to solve problems involving triangles.

Example 1

A triangle ABD is shown below. A vertical line dropped from A intersects the line BD at C. The ratio of the lengths BC:CD is 2:7. What is the distance BD?

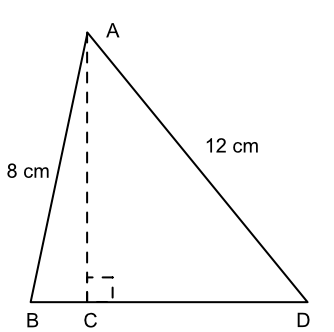
Triangle into two smaller triangles to calculate base

The distance AC is the same for both triangles ABC and ACD

Let the distance BC be 2y and CD be 7y

AC same for both	`sqrt(8^2 - (2y)^2)`	`= sqrt(12^2 - (7y)^2)`
	`8^2 - 4y^2`	`= 12^2 - 49y^2`
	`45y^2`	`= 80`
	`y^2`	`= 1.7778`
	`y`	`= 1.3333`
Length of BD		`= 2y + 7y`
substitute		`= 2(1.3333) + 7(1.333)`
		`= 12`

Answer: 12cm

Example 2

What is the area of the triangle ABC, shown below? Give the answer to 1 decimal place.

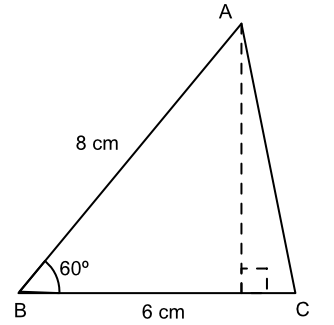
Triangle split into two smaller triangles to calculate area

Draw a vertical from A. Let this be length x

use SOHCAHTOA	`sin`	`=frac(text(opposite))(text(hypotenuse))`
substitute	`sin (60)`	`=frac(x)(8)`
	`6.928`	`= x`
For a triangle	`text(Area)`	`= frac(1)(2) xx bh`
Substitute		`= frac(1)(2) xx 6 xx 6.928`
		` =20.785`
To 1dp		` =20.8`

Answer: 20.8 cm²