A Linear Function represents a constant rate of change. When plotted on a graph it will be a straight line.
A graph may be plotted from an equation `y = mx + c` by plotting the intercept at `(0, c)`, and then drawing the gradient `m`, although it is normally easier to generate the points in a table and plot the graph.
The graph of a line can be used to find the equation by working out the gradient `frac(up)(along)` which gives the `m` value, while the intercept on the y-axis gives the `c` value.
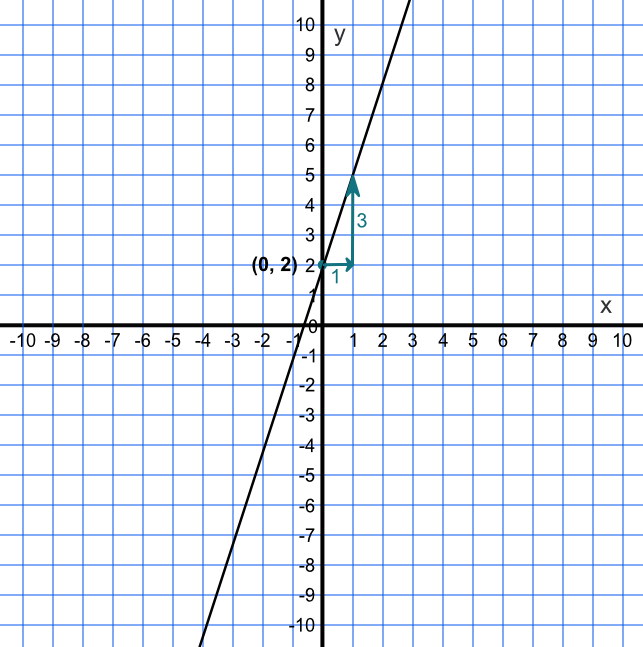
Draw a graph for the equation y = 3x + 2
Either plot a table for values of `x` and `y` or,
Using `y = mx + c`:
`c` is the intercept `y = 2` when `x = 0` and
`m` is the gradient = 3 (3 up, 1 along)
Answer:
Without drawing a graph, determine the coordinates for the intercepts on the `x-` and `y-`axes for `y = 4x - 4`.
When `x = 0`, then `y = 4 xx 0 - 4` therefore `y = -4`. Coordinate is (0, -4)
When `y = 0`, then `0 =4x - 4` therefore `x` = 1. Coordinate is (1, 0)
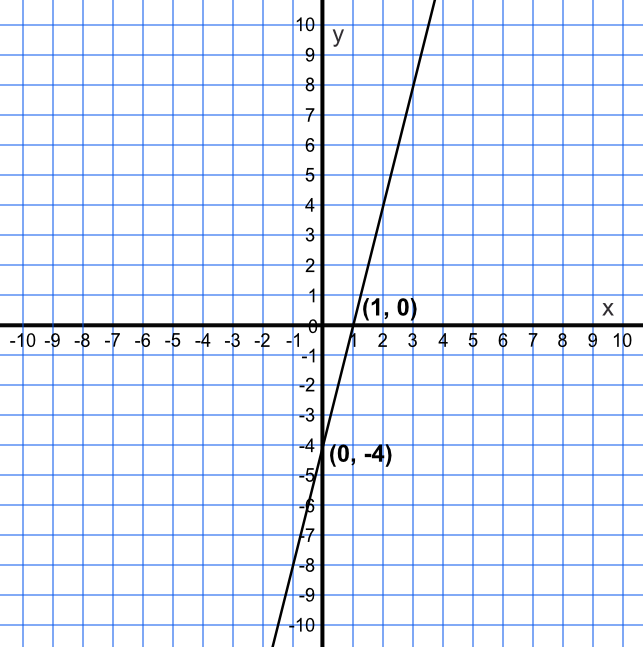
Answer: (0, -4) and (4, 0)