A cubic function will have an `x^3` term. An example of a cubic function is `2x^3 + 8x^2 - 2x - 8`.
A cubic function will have either one, two or three distinct solutions, where the function crosses the x-axis. This can be determined by factorising the function: the above example factorises to `(x + 4)(2x - 2)(x + 1)`, giving roots of -4, 1 and -1. The function `y = (x - 4)^3` has one distinct solution (+4).
The intersection with the `y`-axis can be obtained by identifying the number part of the function.
Sketch the graph of `y = x^3-3x^2-x+3`. Mark the points of intersection with both the `x` and `y`-axis.
Hint: the function factorises to `(x-3)(x-1)(x+1)`.
Substitute a value into each bracket to make that bracket zero eg for the first bracket, set `x`=3 to make `(x-3)=0` therefore `x` is a solution. Similarly for the other two brackets.
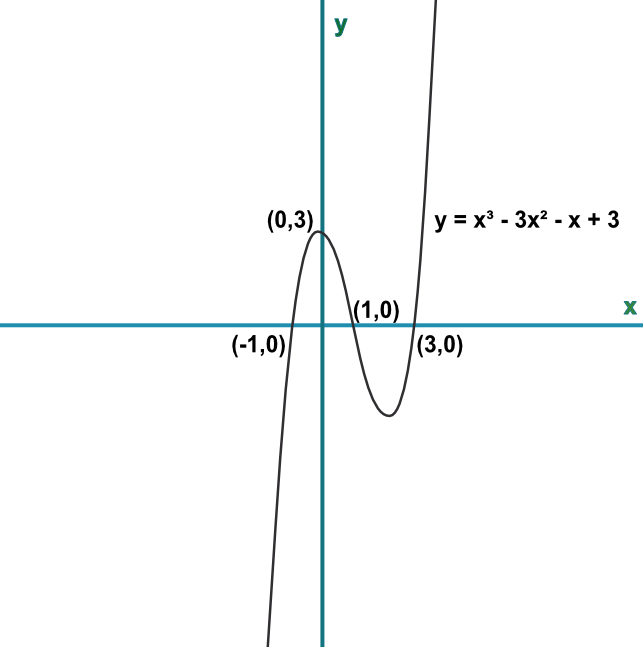
Answer: The roots of the equation are 3, 1 and -1.
How many distinct solutions does `y = x^3 - 1` have?
The only solution to `x^3-1` is when `x`=1
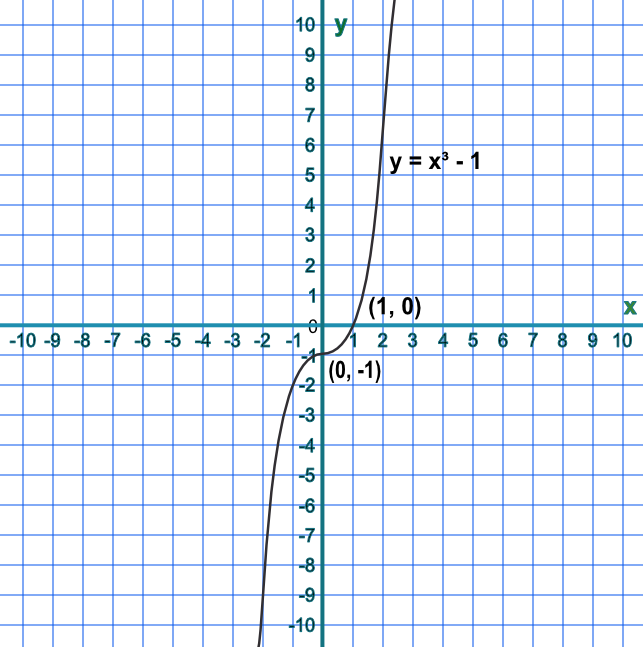
Answer: 1
See also Cubes