A vector `((a),(b))` may be a #position vector# which describes a vector from the origin O to a point (a, b).
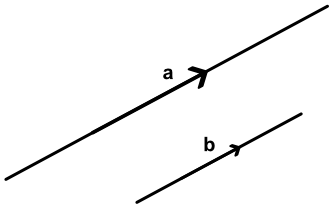
Parallel vectors are vectors that have the same direction but may have different magnitude. In the diagram, below, vectors a and b are parallel, and a = 2b. The multiplier is known as a scalar.
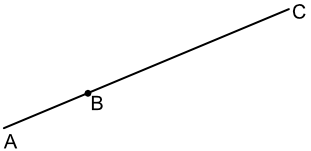
In the diagram below, points A, B and C are on the same line (they are said to be collinear). Vector `vec(AB) = kvec(AC)`, where k is a scalar.
Show that points A at (3, 5), B at (7, 11) and C at (13, 20) are collinear.
The explanation as well as the calculation should be provided.
Answer: `vec(AB) = ((4),(6))` and `vec(AC) = ((10),( 15))`
Let `bb(a) = vec(AB)` and `bb(b) = vec(AC)`
`bb(a) = 2.5bb(b)`
a is a multiple of b and both share at least one point; they are collinear.
Three points are on a straight line AC. Point A is at position (5, 7). Point C is at (-5, 12). Given `vec(AC) = bb(a)` and `vec(AB) = bb(b)`, and `bb(b) = frac(3)(5)bb(a)`, what is the position of point B?
`vec(AC) = ((-10),(5)) `
`vec(AB) = frac(3)(5) xx ((-10),(5)) = ((-6),(3))`
Question asks for the position of point B;
Origin to point A + vector `((-6),(3))` is (5 - 6, 7 + 3) = (-1, 10)
Use a quick sketch if that helps:
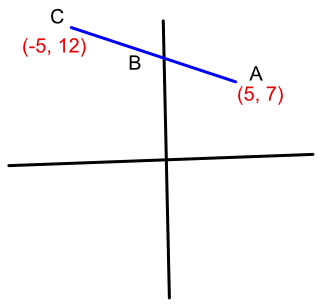
Answer: (-1, 10)