Probability can be presented using tree diagrams. Each branch of the tree represents an outcome (similar to a frequency tree diagram, but each branch is labelled with a probability, not a frequency).
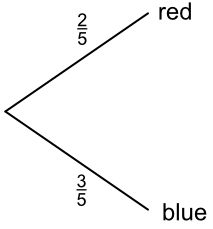
All outcomes must be shown from each node. For example, a bag of balls contains 4 red balls and 6 blue balls. P(red) = `frac(2)(5)` and P(blue) = `frac(3)(5)`:
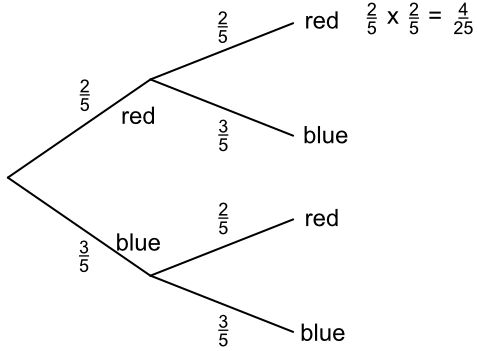
If, in the above example, a ball is drawn, replaced and then a second ball is drawn:
It is important to determine whether, on a subsequent event, whether this depends on the result of the previous event.
Multiply the probabilities along branches to calculate the probability of two consecutive events. The probability of drawing two red balls is P(red) x P(red) = `frac(2)(5)` x `frac(2)(5)` = `frac(4)(25)`.
If the balls were NOT replaced, then the denominator on the second event as there are fewer bags in the ball to draw from. This gives a different answer:
Adding the ends of all the branches gives a probability of 1.
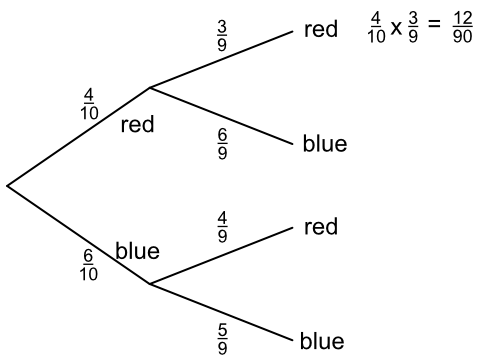
A bag contains 12 balls. 3 are red and 9 are blue. A ball is drawn at random, and replaced in the bag. A second ball is drawn at random. What is the probability of drawing 2 red balls?
Draw the probability tree. For two red balls, multiply along the tree:
P(red) x P(red) = `frac(3)(12)` x `frac(3)(12)` = `frac(9)(144)` = `frac(1)(16)`
Answer: `frac(1)(16)`
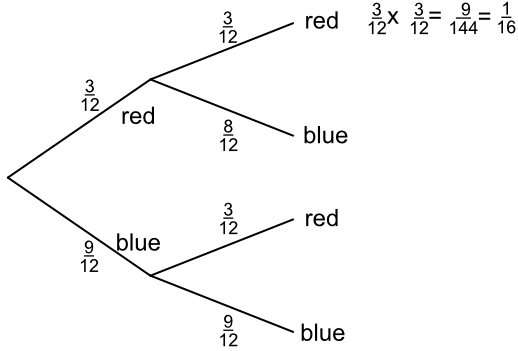
A bag contains 12 balls. 3 are red and 9 are blue. A ball is drawn at random, and NOT replaced in the bag. By drawing a probability tree, or otherwise, show that the probability of drawing two consecutive balls of the same colour is `frac(21)(33)`.
Note that the balls are NOT replaced: therefore the denominator of the fractions changes between the first draw and the second draw.
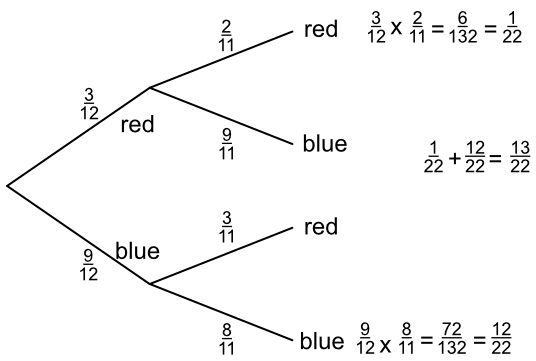
Answer: Probability of two reds or two blues:
(P(red1) x P(red)2) + (P(blue)1 x P(blue)2)
`frac(3)(12)` x `frac(2)(11)` + `frac(9)(12)` x `frac(8)(11)` = `frac(13)(22)`
See also Independent and Dependent Events