Ratios are used to determine similarity between geometric shapes.
Two triangles are shown in the diagram: ABC and ADE. The lines BC and DE are parallel. All the angles in the triangle are equal, and therefore the triangles are similar.
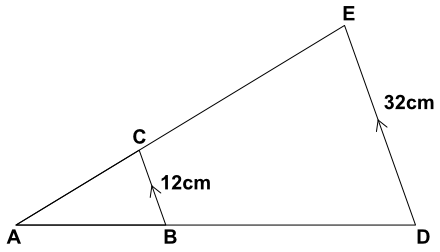
The ratios of the lengths of the sides BC : DE are 12 : 32, which can be simplified to 3 : 8.
The other lengths are all in same ratio If AB is 24cm, then AD is `frac(24 xx 8)(3)` = 64cm.
If, on the above diagram, AC is 22cm, then what is the length AE?
The ratio for the lengths is 3 : 8. AC is 22cm, the length AE is `22 xx 8/3` = 58.67cm
Answer: 58.67cm
Two drawings have been produced for a part in a machine. One drawing is at a scale of 1:100, and the area of the part is 5 cm2. The second more detailed drawing is at a scale of 1:50. What is the area of the part on the detailed drawing?
The linear scale is 2 (each length on the detailed drawing is twice as large).
The area scale is 22 = 4.
The area of the part on the first drawing is 5cm: the area of the part on the second drawing is 5 x 4 = 20cm2.
Answer: 20cm2