There may be 0, 1 or 2 roots for a quadratic. A root is found for `x` when `f(x)=0`. This can be seen graphically when the curve crosses `y=0`. If the curve does not cross `y=0` then there are no real roots for the function.
The roots can be obtained by:
• rearranging as factors; (Factorising)
• using the quadratic formula `x = frac(-b +- √(b^2 - 4ac))(2a)`; (Quadratic Formula)
• completing the square; (Completing the Square)
• deducing iteratively (for a positive square root)
• and for an approximate solution: drawing a graph of the function.
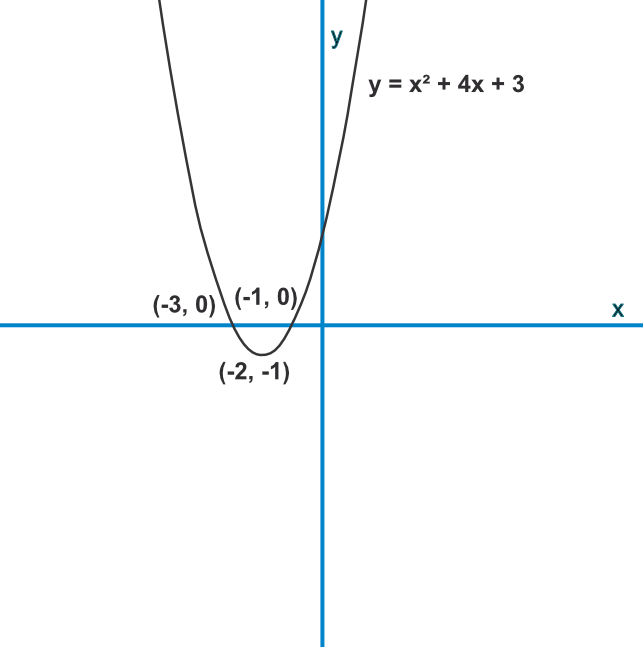
Sketch the graph of `x^2 +4x + 3` showing the coordinates of the roots and the turning point.
Factorise the equation to `(x+3)` and `(x+1)`. This gives the roots as `x=-3` and `x=-1`
The turning point is given using `-frac(b)(2a) = frac(-4)(2(1)) = -2` This is the `x` value, substitute into the original equation for `(-2)^2 +4(-2)+ 3 = 4 - 8 + 3 = -1`
Roots are (-3,0) and (-1, 0); turning point is (-2,-1)
Answer:
The roots of a quadratic are -5 and 7. The turning point is (1, -36). The coefficient of the squared term is 1. What is the quadratic?
The roots give the factors of the expression `(x + 5)(x - 7)`
Multiply that out to give `x^2 - 2x - 35`
Check with the turning point: `-36 = (1)^2 - 2(1) - 35`✔
Answer: `x^2 - 2x -35`