Sin

Trigonometrical ratios are the relationship between an angle and the three sides of a right angled triangle.

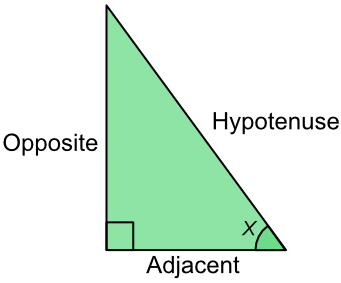
Sin showing names of sides relative to angle

The ratio of the opposite side to the hypotenuse is the sine of the angle, shortened to sin. The opposite side is the side opposite the angle.

`Sin(x) = frac(text(Opposite))(text(Hypotenuse))`

This is SOH part of the mnemonic SOH CAH TOA, and gives you the formula above.

If an angle and either the hypotenuse or opposite side are known, the formula can be used to get the missing length. Use the sin key on your calculator to get the sin value for the angle.

If the two lengths (hypotenuse and opposite) are known, then carry out the division. The formula gives you the sin value for the angle. Use the sin^-1 key on your calculator to get the value of the angle.

The sin key on your calculator changes the angle to the sin value of the angle.

The sin^-1 key on your calculator is the inverse, and lets you go from the sin value of the angle to the angle itself.

Example 1

What is the length of AB?

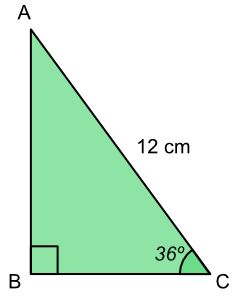
Work out Sin with angle and hypotenuse

SOH	Sin `(x)`	`= frac(text(Opposite))(text(Hypotenuse))`
substitute	`sin (36)`	`=frac(AB)(12)`
find sin(36)	`0.578`	`=frac(AB)(12)`
x12 both sides	`0.578 xx 12`	`= AB`
	`7.053`	`= AB`

Answer: 7.053 cm

Example 2

What is the value of the angle `x`?

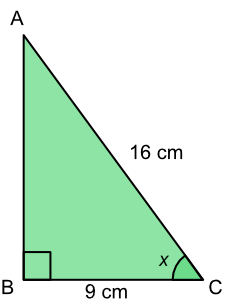
Work out angle with adjacent and hypotenuse

SOH	Sin `(x)`	`=frac(text(Opposite))(text(Hypotenuse))`
substitute	`sin (x)`	`=frac(9)(16)`
	`sin (x)`	`=0.5625`
sin^-1 both sides	`x`	`=sin^-1 (0.5625)`
		`= 34.23º`

Answer: 34.2º