Graphs can be translated horizontally and vertically.
To translate the graph horizontally, add or subtract a value before the function is applied. The movement is in the opposite direction to the value of the addition or subtraction. If `y = f(x)` then `f(x + a)` will cause the graph to be translated by `((-a),(0))`.
To translate a graph vertically, add or subtract a value after the function is applied. That is, if `y=f(x)` then `y=f(x)+a` will result in a translation of `((0),(a))`.
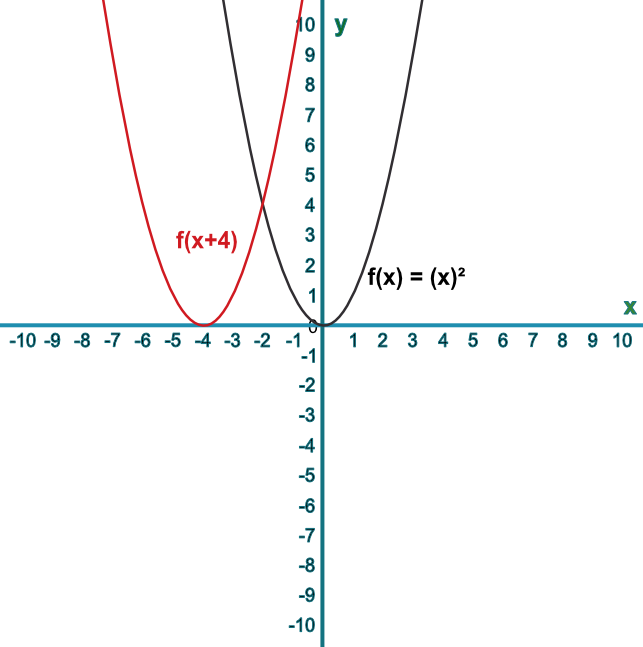
Sketch the graph of `f(x)=x^2`. Then sketch the graph of `f(x+4)`.
Describe the translation.
To translate a function horizontally, apply the add/subtract before evaluating the function.
Answer: The line has been translated `((-4),(0))`
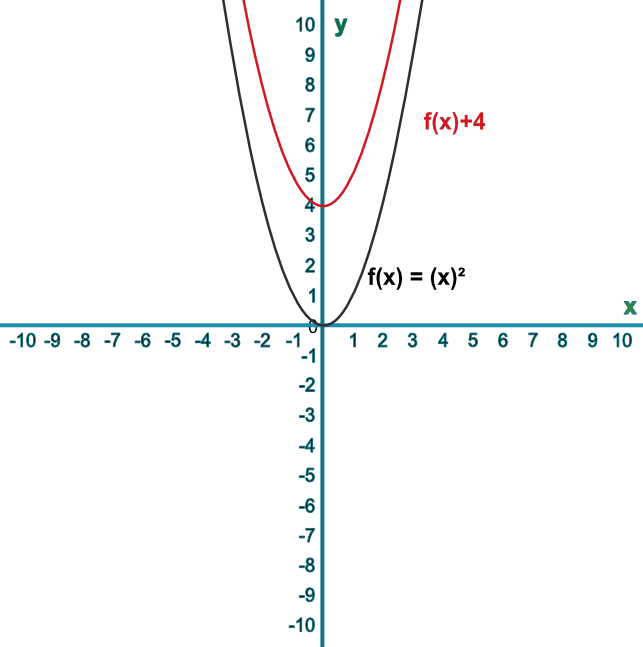
Sketch the graph of `f(x)=x^2`. Then sketch the graph of `f(x)+4`.
Describe the transformation.
To translate a function vertically, apply the add/subtract after evaluating the function.
Answer: The line has been translated `((0),(4))`
See also Expressions as Functions and Translation