The circle theorems are:
The angle between a tangent and a radius is 90º.
Tangents drawn to a point outside the circle have equal lengths.
A perpendicular from a chord to the centre of a circle bisects the chord.
The angle at the centre of the circle is twice the angle at the circumference when subtended by the same arc.
The angle in a semicircle is 90º.
Angles subtended at the circumference by the same arc are equal.
Opposite angles of a cyclic quadrilateral add to 180º.
An exterior angle of a cyclic quadrilateral is equal to the opposite interior angle.
The angle between a tangent and a chord is equal to the opposite interior angle.
ABCD is a cyclic quadrilateral. O is the centre of the circle. The angle ∠ADC is 116º: what is the value of the angle ∠AOC?
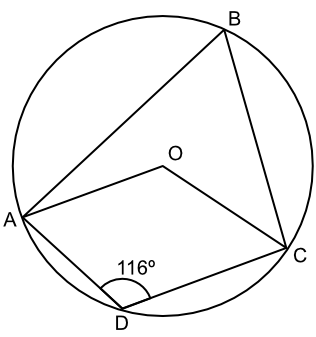
Opposite angles in a cyclic quadrilateral add to 180º: ∠ABC = 180 - 116 = 64º.
Angle at the centre is twice the angle at the circumference when subtended by the same arc: 64 x 2 = 128º.
Answer: 128º
AB and BC are tangents to the circle with centre O. D is a further point on the circumference. The angle ABC is 65º.
What is the value of the angle ∠ADC?
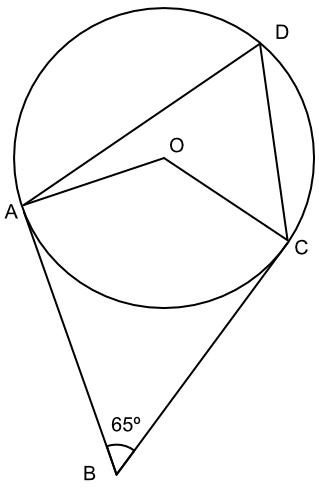
AO and OC are radii and are at right angles to the tangents.
AOCB is a quadrilateral; AOC = 360 - 65 - 90 - 90 = 185º
Angle at the centre is twice the angle at the circumference when subtended by the same arc: 185 ÷ 2 = 92.5º.
Answer: 92.5º