A prism is a shape where the cross-sectional area remains the same throughout the length of the prism.
The surface area of a prism consists of the two ends, plus the surface area of the length.
Calculate the surface area of the two ends. Then work out the perimeter of one end, and multiply this perimeter by the length of the prism.

A right triangular prism (a triangular prism with a right angle) has sides of length 3cm, 4cm and 5cm. The prism is 15 cm long.
What is the surface area of the prism?
The surface area = surface area of both ends + surface area along length
Work out the surface area of the end:
The area of each trianglular end = `frac(1)(2)bh`
Area of a triangle = `frac(1)(2) xx 3 xx 4`
Atriangle = 6 cm2
Work out the surface area of the length:
The perimeter of the triangle = 3 + 4 + 5 = 12 cm.
Surface area along length = area of end x length
Alength = 12 x 15 = 180
Work out the total:
Surface area = surface area of both ends + surface are along length
Surface area = 2 x Atriangle + Alength
Surface area = 192
Answer: 192 cm2
A prism is in the shape of a hexagon. The area of one end is 43.81 cm2. The surface area of the entire prism is 500 cm2. If the length of the prism is 40cm, what is the length, x, of one edge of the hexagon shape? Give your answer to 1 decimal place.
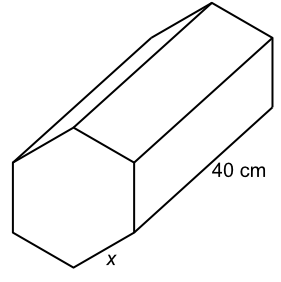
| Surface Area prism | = 2 x end areas | + length x perimeter |
| 500 | = 2 x 43.81 | + 40 x p |
| 412.38 | = 40p | |
| p | = 10.3095 |
There are six sides to a hexagon
10.3095 ÷ 6 = 1.71 cm
Answer: 1.7 cm