If the coefficient (the multiple) of the `x^2` term is positive, then the turning point is a minimum. If negative, the turning point is a maximum.
A quadratic curve is vertically symmetrical about its turning point, or vertex.
The `x`-value for the turning point is given by `-frac(b)(2a)` for a function `ax^2+bx+c`. Substituting this value into the equation gives the `y`-value.
What are the coordinates for the turning point for the equation `y = -2x^2 - 4x + 6`?
The `x`-value is given by `-frac(b)(2a)` = `-frac(-4)(2 xx -2) = -1`.
Substituting `-2(-1)^2 - 4(-1) + 6 = -2 + 4 + 6 = 8`
Answer: (-1,8)
Is the turning point a maximum or a minimum?
The coefficient for the squared term is negative, so the turning point is a maximum.
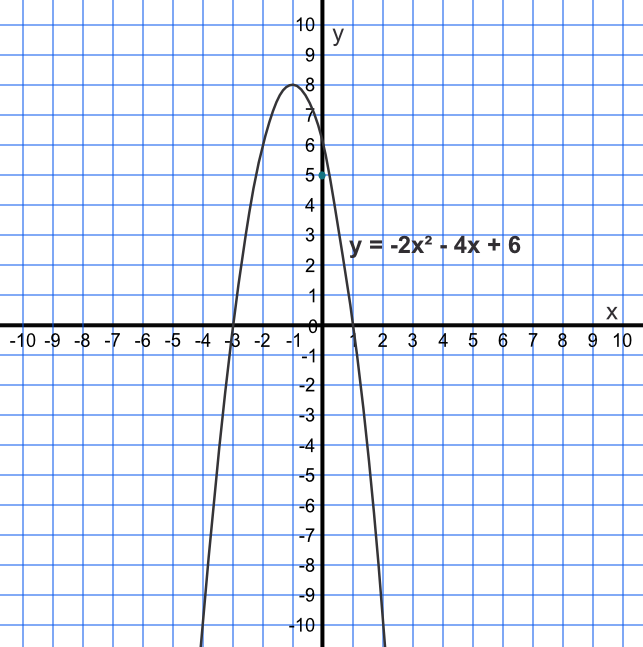
Answer: A maximum.
See also Completing the Square