Geometric Proofs use a logical argument that always follows the same form.
Proofs start with a Given fact about the problem being solved. There then follows one or more steps, which consist of a Statement followed by the Reason that that statement is true.
The final statement is the fact being proven.
For the parallelogram given below, prove that angle CAB is congruent to angle BDC. You may assume that opposite sides in a parallelogram are equal.
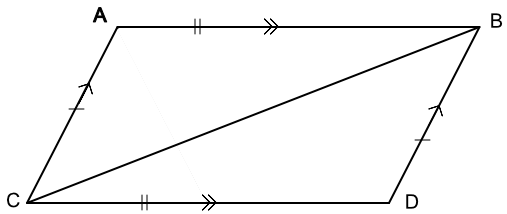
Answer: Given: Opposite sides in a parallelogram are equal
| Statement | Reason |
|---|---|
| AB = CD | Opposite sides in a parallelogram are equal |
| AC = BD | Opposite sides in a parallelogram are equal | BC is shared | Line BC shared by both triangles | Triangles are congruent | Congruency by SSS | therefore ∠CAB = ∠BDC |
Prove that, for the triangle below, a line drawn at a right angle from the midpoint of AB (point D) bisects the angle at C.
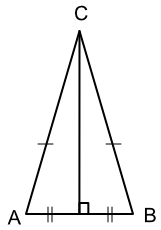
Answer: Given: The triangle is isosceles; D is the midpoint of AB
| Statement | Reason |
|---|---|
| DC is common | Line shared by both smaller triangles |
| AC = CB | Definition of an isosceles triangle |
| AD = DB | D is given as the midpoint |
| Triangles are congruent | Congruency by SSS |
| ∠ACD = ∠DCB | ∠ACB is bisected |
See also Congruent Triangles