Probability Venn Diagrams

Probability events can be allocated to sets. The sets can then be analysed by using Set Theory or Venn Diagrams.

The universal set consists of all possible events.

For a given outcome, all the events that are possible for that outcome will belong to the same set.

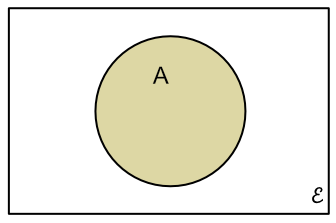
Single probability in a Universal Set

The probability of a given outcome is:

P(outcome) = `frac(text(number of members of set))(text(number of members in universal set))`

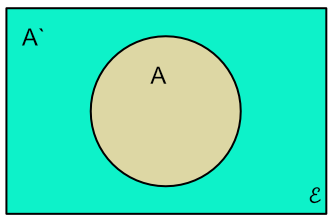
The probability of an event A not happening is P(not A). In set terms, this is shown as

P(A`),

and P(A) + P(A`) = 1.

Probable and not probable in a Universal Set

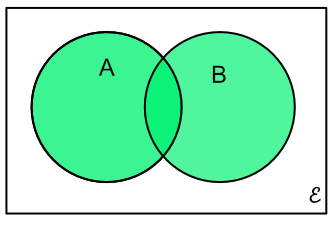
When a probability can be an outcome in A AND B (A #intersection# B, or `A nn B`) then the overlap of sets A and B are considered.

Probability of both events happening in a Venn Diagram

When a probability is being considered where an event can be in either outcome A OR B then all the elements in A and B are considered (elements in A #union# B, or `A uu B`: note that elements in both A and B are counted only once.

Probability of either event happening in a Venn Diagram

Example 1

Two fair dice are thrown. Using a Venn Diagram, what is the probability of `O uu P` where O is the set of odd numbers and P is the set of Prime numbers?

`epsilon`	= {2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
`text(O)`	= {3, 5, 7, 9, 11}
`text(P)`	= {2, 3, 5, 7, 11}
`O uu P`	= {2, 3, 5, 7, 9, 11}

Number of events = 11

P(`O uu P`) = `frac(6)(11)`

Answer: `frac(6)(11)`

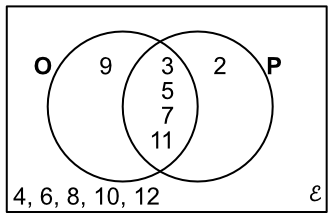
Probability of throwing odds or primes in a Venn Diagram

Example 2

With the Venn Diagram, above, what is the probability of `O nn P`?

`O nn P = {3, 5, 7, 11}` = 4 events

`epsilon` is 11 events

P`(O nn P) = frac(4)(11)`

Answer: `frac(4)(11)`