The roots of the function are found when `y` = 0 (that is, the curve crosses the `x`-axis).
A quadratic may cross the `x`-axis twice, or it may only touch the `x`-axis, or it may not cross the `x`-axis at all. In the first instance, the quadratic will have two roots; in the second instance there will be one root (actually the same root repeated); and in the third instance no real roots (the graph does not cross `y` = 0).
The values of `x` when it crosses the `x`-axis are the solutions to the equation.
By drawing a graph, estimate the roots for `y = x^2 - 5x + 6`.
| `x` | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| `x^2 - 5x + 6` | 12 | 6 | 2 | 0 | 0 | 2 | 6 | 12 |
Answer: `x=2` and `x=3`
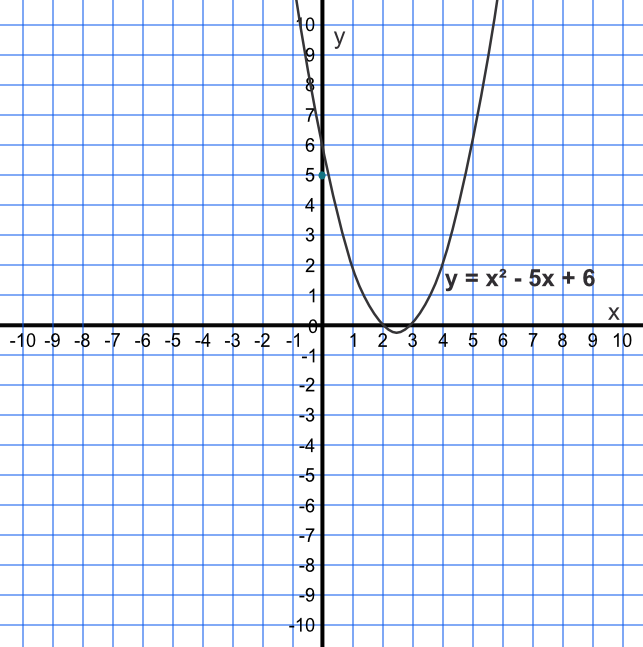
With the two roots from the answer, above, show that they are valid roots.
The roots are given where the line crosses the `x`-axis, at (2,0) and (3,0)
When `x=2` or `x=3` then `y=0`
Answer:
Substituting 2 into the function: (2)2 - 5(2) + 6 = 4 - 10 + 6 = 0, therefore a root
Substituting 3 into the function: (3)2 - 5(3) + 6 = 9 - 15 + 6 = 0, therefore a root