Higher
There are two sides to proving an algebraic statement. To prove a statement is true, it must be true for every case. To prove a statement is false, it is only necessary to prove it is false for a single case.
Taking the false statement first: Is the statement All prime numbers are odd numbers true or false? The number 2 is a prime number: it can be divided by 1 and itself, and it is even. Therefore the statement is false.
Proving a statement is true requires defining general cases. Proof tends to fall into two categories: arithmetic proofs and algebraic proofs. Arithmetic proofs rely on two facts, and may be taken as true:
2n, where n is a positive integer, is always even;
therefore 2n + 1 is odd;
the sum of an odd and an even number is odd;
as addition is commutative, the sum of an even and an odd number is also odd.
Arithmetic proofs will often be made by substitution. For example: prove that adding two consecutive even numbers will always be even:
Let the two numbers be 2n and 2n + 2;
= 4n + 2
= 2(2n + 1); the number is divisible by 2 and therefore an even number.
Algebraic proofs will rely on building an expression from given facts, or rearranging expressions to prove identities.
1. Show that the product of two consecutive odd numbers will always be odd.
Answer:
Let the numbers be 2n + 1 and 2n + 3
(2n + 1)(2n + 3)
= 4n2 + 4n + 3
= 2(2n2 + 2) + 3
The expression in brackets is a factor of 2; and the remainder is an odd number. An even number added to an odd number is always odd.
2. A circle has a radius x. A smaller circle, of radius x - 2, is removed from the circle. The area of the shape that is left is 16π.
Show that x - 5 = 0.
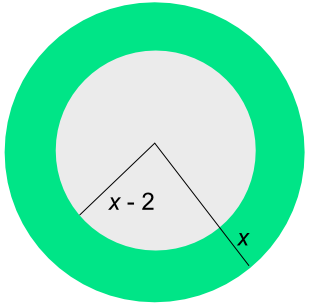
Answer:
The area of the larger circle is πx2.
The area of the smaller circle is π(x - 2)2.
The area left is πx2 - π(x - 2)2
= πx2 - π(x2 - 4x + 4)
= πx2 - πx2 + 4πx - 4π
= 4π(x - 1)
The area of the circle is given as 16π, therefore 4π(x - 1) = 16π
therefore x - 1 = 4, or x - 5 = 0.