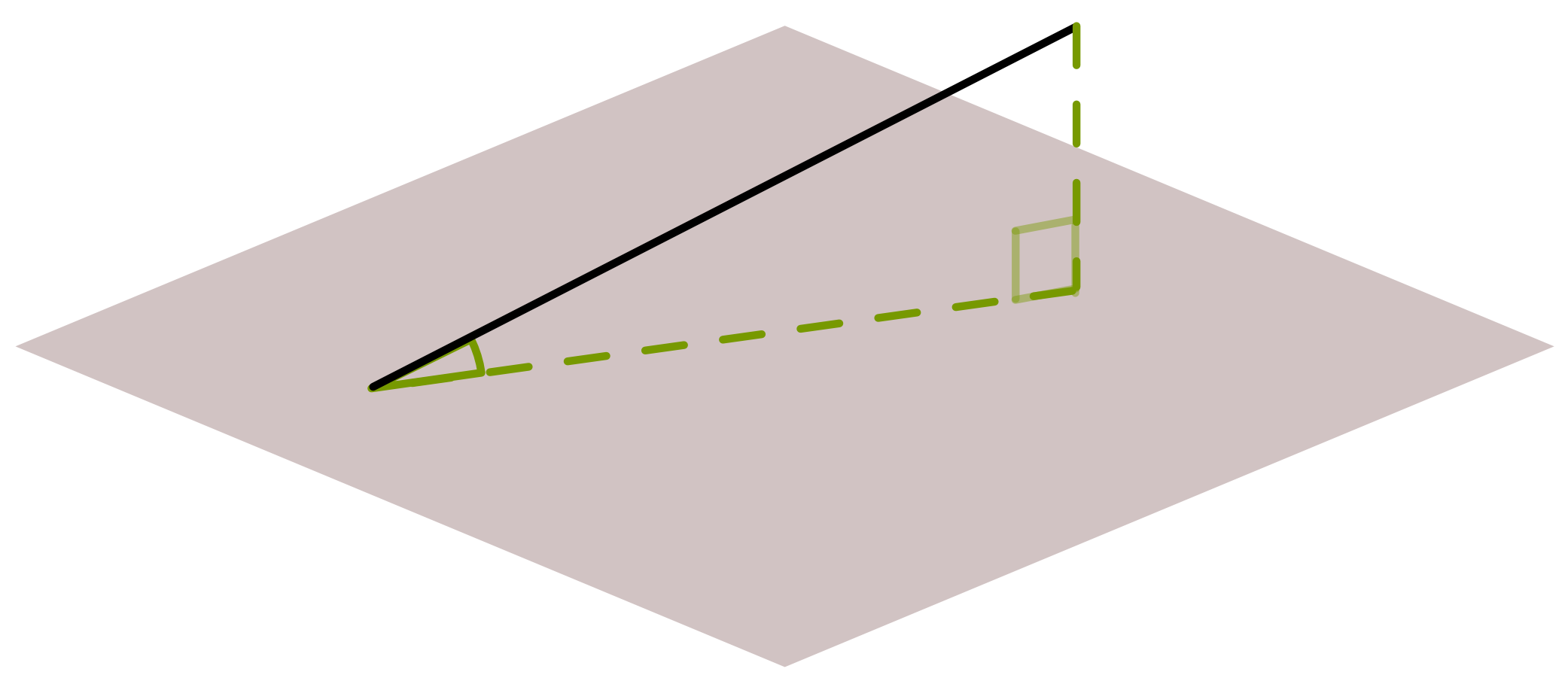
A line that intersects a plane makes an angle to the plane. The angle is defined by taking a point on the line and dropping it vertically to the plane. Complete a triangle by drawing from this point to where the line intersects the plane. The angle is then defined by the triangle.
A triangular prism has sides of 5cm and 7cm and is 10cm long.
What, to the nearest degree, does the line EB make with the base ABCD of the prism?
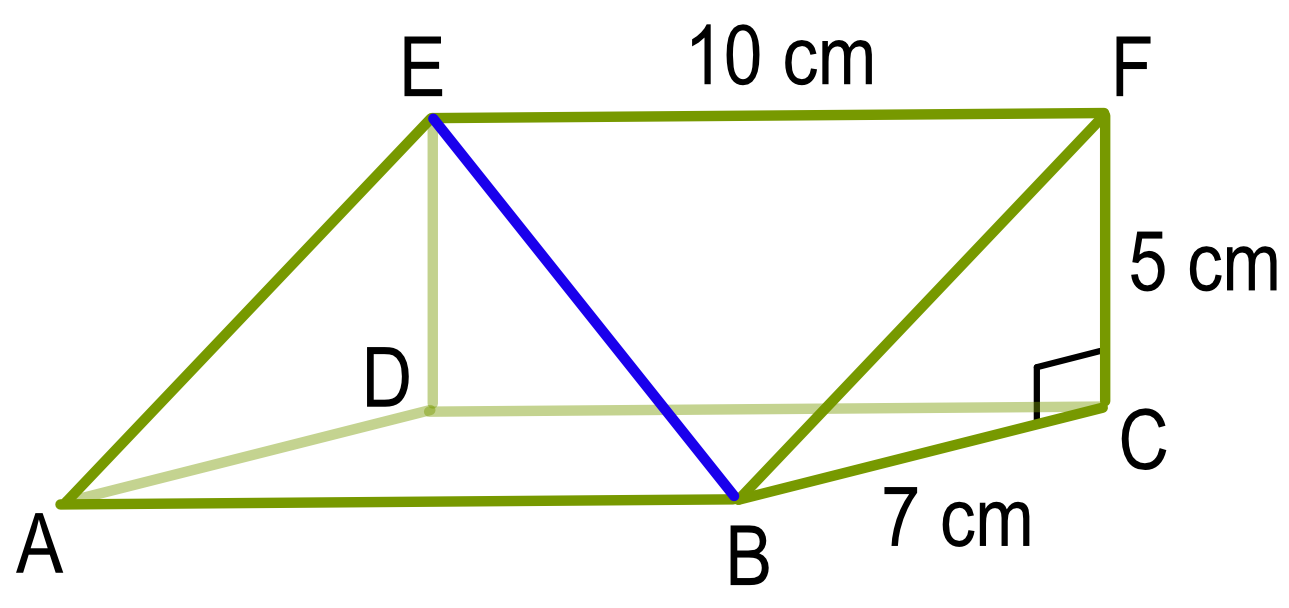
Calculate the length of the line DB by using Pythagoras` theorem.
Then use SOH CAH TOA to determine the length: as the adjacent (DB) and opposite (DE) lengths are known, it is the TOA part that is used.
| Pythagoras | `c^2` | `= a^2 + b^2` |
| substitute | `AB^2` | `= 7^2 + 10^2` |
| `AB` | `= sqrt(149)` | |
| `= 12.2066` | ||
| TOA | `tan x` | `= frac(text(opposite))(text(adjacent))` |
| substitute | `= frac(5)(12.2066)` | |
| `= 5.385` | ||
| tan_1 both sides | `x` | `= 22.27` |
| nearest degree | `= 22` |
Answer: 22º
A line is extended from the centre of the base O of a cuboid to one corner E. What angle does the line EO make with the base of the cuboid ABCD? Give your answer to 1 decimal place.
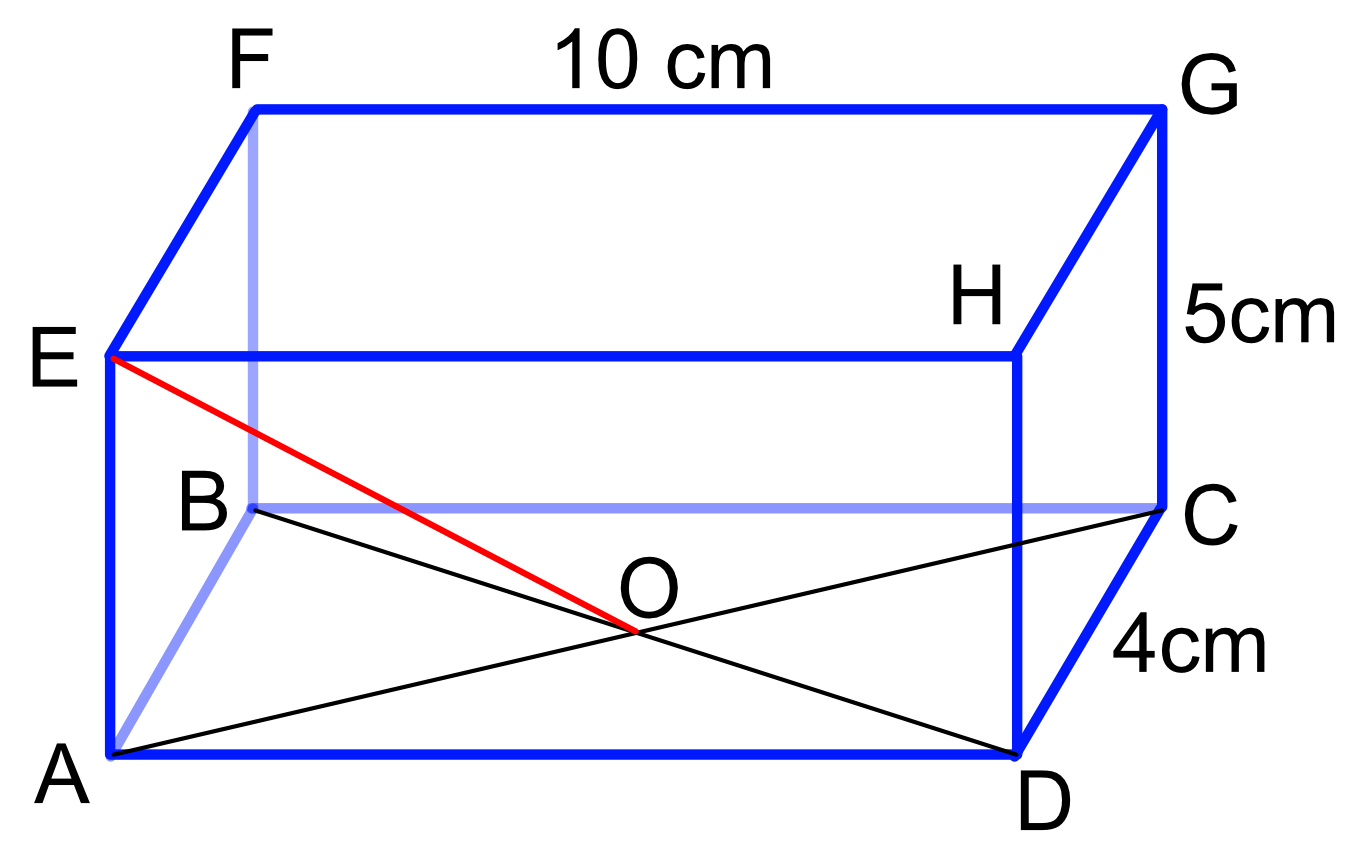
Calculate the length of the line AO by using Pythagoras` theorem.
Then use SOH CAH TOA to determine the length: as the adjacent (AO) and opposite (AE) lengths are known, it is the TOA part that is used.
| Pythagoras | `c^2` | `= a^2 + b^2` |
| substitute | `AB^2` | `= 2^2 + 5^2` |
| `AB` | `= sqrt(29)` | |
| `= 5.385` | ||
| TOA | `tan x` | `= frac(text(opposite))(text(adjacent))` |
| substitute | `tan x` | `= frac(5)(5.385)` |
| `= 0.928` | ||
| tan-1 both sides | `x` | `= 42.87` |
| nearest degree | `= 43` |
Answer: 43º