WTMaths logo
Area of Any Triangle

Area of Any Triangle

The area of a triangle is `A = frac(1)(2)bh`, where `b` is the base length and `h` is the vertical height.

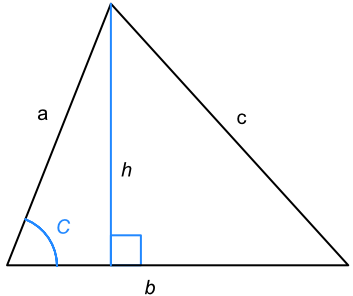
Area of any Triangle

Using the trigonometrical ratios, the vertical height `h = a xx sin C`.

Substituting into the formula for the area of a triangle when the vertical height is known:

`A = frac(1)(2) xx b xx h`

`A = frac(1)(2) xx b xx a xx sin C`

`A = frac(1)(2)ab sin C`

Example 1

What is the area of the triangle, below? Give your answer correct to 2 decimal places.

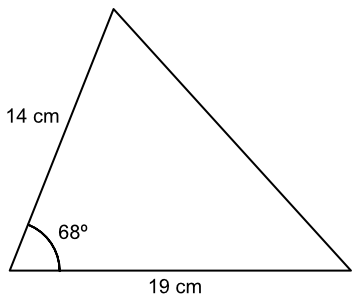
Work out the area of a given triangle

Area of a triangle `A` `= frac(1)(2)ab sin C`
substitute `= frac(1)(2)(14)(19) sin (68)`
`= 123.3155`
to 2 dp `= 123.32`

Answer: 123.32 cm2

Example 2

The area of the triangle below is 100 cm2. What is the size of the angle x? Give your answer correct to the nearest degree.

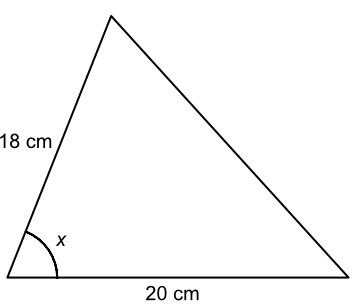
Work out the angle of a triangle given an area

Area of a triangle `A` `= frac(1)(2)ab sin C`
substitute `100` `= frac(1)(2)(18)(20) sin x`
`100` `= 180 sin x`
`0.55556` `= sin x`
sin-1 both sides `sin^-1(0.55556)` `= x`
`33.749` `= x`
nearest degree `34` `= x`

Answer: 34ยบ