An arc is a fraction of the circumference of a circle.
The amount of the circumference that is the arc is given by the number of degrees at the centre.

The circumference of the whole circle is given by `2pir`, and the angle at the centre is 360º.
If the angle of the arc is 83º, then the fraction is `frac(83)(360)` of a whole circle:
The arc length is therefore `frac(83)(360) xx 2pir`.
Note that if the perimeter of the sector is required, then include the two radii: `frac(83)(360) xx 2pir + 2r`.
The area of a whole circle is `pir^2`. The area of a sector uses the same fraction: `frac(83)(360) xx pir^2`.
What is the area of the sector, shown below?
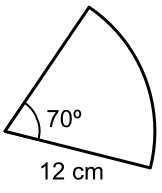
| Area of a circle | A | `= pir^2` |
| Area of this sector | A | `= frac(70)(360) xx pir^2` |
| Substitute | A | `= frac(70)(360) xx pi xx 12^2` |
| `= 87.96` |
Answer: 87.9 cm2
What is the length of the perimeter of the sector shown below? Give your answer to 1 decimal place.

| Perimeter of a circle | P | `= 2pir` |
| Perimeter of a sector | P | `= frac(70)(360) xx 2pir + 2r` |
| Substitute | P | `= frac(70)(360) xx 2pi(12) + 2(12)` |
| `= 14.65 + 24` | ||
| `= 38.66` | ||
| round to 1dp | `= 38.7` |
Answer: 38.7 cm