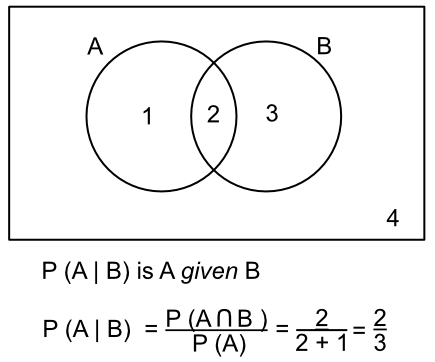
Venn diagrams are used to determine conditional probabilities. The conditional probability is given by the intersections of these sets.
Conditional probability is based upon an event A given an event B has already happened: this is written as P(A | B) (probability of A given B).
The probability of A, given B, is the probability of A and B divided by the probability of A:
P(A) = `frac(text(P)(A nn B))(text(P)(B))`
In Venn diagrams, this is the intersection set divided by the set being considered.
The Venn diagram shows students that are studying a Science subject. The Venn diagram shows those studying Biology and Chemistry. What is the probability of a student studying Biology if they are also studying Chemistry?
Probability of Biology given Chemistry: P(B | C)
The number of students studying Biology and Chemistry = P(B nn C) = 13 students
The total number of students studying Chemistry = P(C) = 27
P(B | C) = `frac(text(P)(B nn C))(text(P)(C))` = `frac(13)(27)`
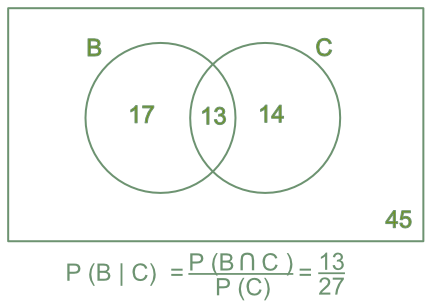
Answer: P(B | C) = `frac(text(P)(B nn C))(text(P)(C))` = `frac(13)(27)`
The Venn diagram shows students that are studying a language subject (French, Spanish and German). What is the probability of a student studying three subjects, given that they are studying at least two subjects?
Taking at least two languages = 6 + 5 + 7 + 4 = 22
P(3lang | 2lang) = P`frac(text(students taking 3 languages))(text(all students taking 2 or more languages))` = `frac(7)(22)`
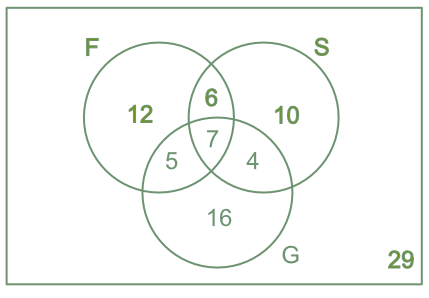
Answer: P(three languages | two languages) = `frac(7)(22)`