A frequency tree can be used to determine how many combinations of one or more events can take place. In its simplest form, a frequency tree consists of two branches.
Consider a bag of red and blue balls. If there are 6 red balls and 4 blue balls, the tree diagram will show:
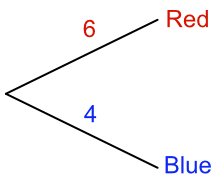
The diagram shows that there are 6 ways to pick a red ball, and 4 ways to pick a blue ball.
If a red ball was picked and then placed back in the bag; and another ball was picked, the diagram could be extended:
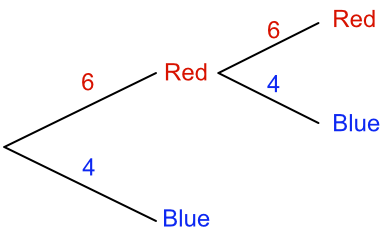
The number of ways of picking a red ball, followed by another red ball is found by multiplying along the branches concerned: 6 x 6 = 36 ways of picking a red ball followed by another red ball.
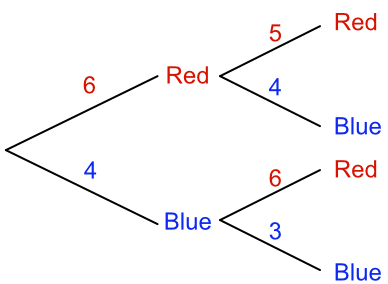
If the ball is not replaced in the bag, then the number of red balls available for the second selection changes, and the number of ways of picking a red ball becomes 6 x 5 = 30 ways:
A bag of chocolates is offered to Amelia. In the bag there are 5 white chocolates, and 7 milk chocolates. Draw a frequency tree for Amelia as she selects her chocolate.
Answer: 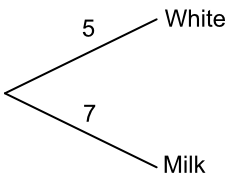
Amelia chooses a chocolate, then replaces it in the bag. She then chooses again. How many different ways can she choose a white chocolate, followed by another white chocolate?
From the frequency tree, 5 x 5 = 25
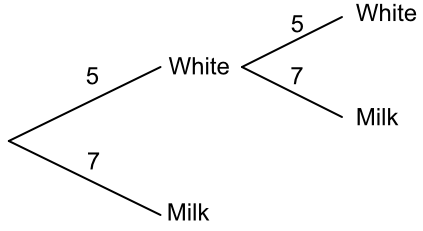
Answer: 25