Inequalities in rounding can be shown using either number lines or expressions. For example, the number of students in a class may be 20 to one significant figure. The minimum number of students in a class would be 15 (15 rounds up to 20). The maximum number of students would be 24: any more, and it would round up to 30.
You can write this as 15 ≤ students < 25: that is, the number of students in the class is greater than or equal to 15; and less than 25. On a number line it would look like this;
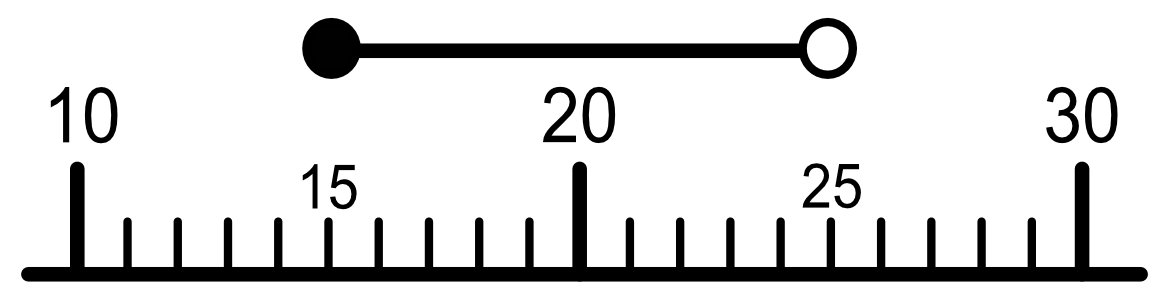
The circle at one end of the line is filled in, which indicates that the value (15) is included. The circle at the other end is not filled in, which shows that the value (25) is not included.
The example given above deals with rounding for integers. If, instead, a number, n, was given as 23.4 to 1 decimal place, then the original number could have been as small as 23.35000... or as large as 23.4499999... The expression is 23.35 ≤ n < 23.45: that is, n is equal to or greater than 23.35, but less than 23.45:
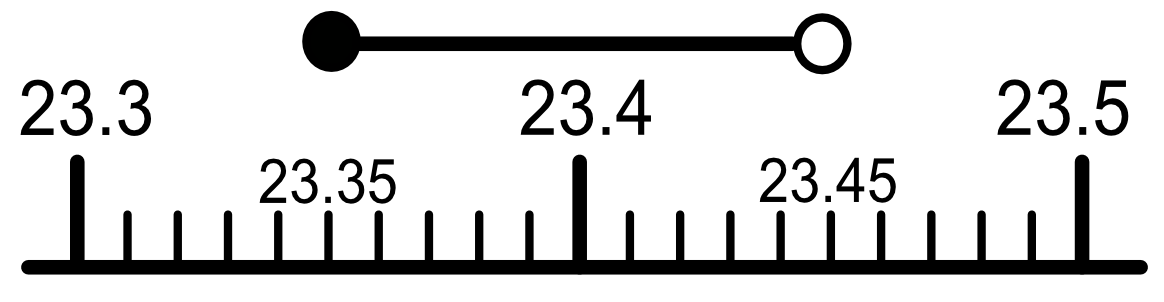
Again, the circle at the right hand end is not filled in, which indicates that the number 23.45 is not included in the inequality.
A tyre is being pressurised and the digital display is showing 29.6 pounds per square inch. The display rounds to 1 decimal place.
What could the range of pressure be for the tyre? Show the answer as an inequality.
Minimum pressure: 29.55, rounds up to 29.6.
Maximum pressure is just below 29.65 (e.g. 29.64999..), rounds down to 29.6
Answer: 29.55 ≤ pressure < 29.65
A pilot is given an instruction by Air Traffic Control to fly at 23,000 feet. His altimeter, which tells him how high he is flying, is accurate to 3 significant figures.
What is the actual range of heights that he might be flying at? Give the answer as an inequality.
Minimum height is 22,950 feet: any less and it would round down to 22,900.
Maximum height is 23,049.999... feet. Any more and it would round up to 23,100
Answer: 22,950 ≤ height < 23,050
See also Inequalities on a Number Line