The midpoint of a line segment is the halfway point between the two ends of a line. You can work it out by adding the two `x`-coordinates together and dividing by two to get the `x`-coordinate of the midpoint; and then repeat with the `y`-coordinate.
The formula for the midpoint of a line segment is `(frac(x_1+x_2)(2), frac(y_1 + y_2)(2))`.
What is the midpoint between (3,11) and (7,15)?
Add the two `x`-coordinates then divide by two = `frac(3 + 7)(2)` = 5
Add the two `y`-coordinates then divide by two = `frac(11 + 15)(2)` = 13
Midpoint coordinate is (5, 13)
Answer: (5, 13)
A line segment is drawn from (-5,-10) to (1,-4). A perpendicular line passes through the midpoint of this line segment.
What is the value of the `y`-coordinate on the perpendicular line when `x` = 0?
Work out the equation of the line segment as `y=mx+x`
gradient = `frac(6)(6)` = 1
For the point (-5, -10)
`-10 = 1 xx -5 + c`
`c = -5`
Check with other point: -4 = 1 x 1 - 5 ✔
Line segment has equation `y=x - 5`
Midpoint of line segment: `x=frac(-5 + 1)(2) = -2`
And `y = frac(-10 + -4)(2) = -7`
Midpoint is therefore (-2, -7)
The perpendicular line has a gradient of `frac(-1)(m) = frac(-1)(1) = -1`
Perpendicular line passes through the point (-2, -7) and substituting
`-7 = -1 x -2 + c` gives `c=-9`
And the equation of the perpendicular line is `y = -x - 9`
When `x` = 0, `y` = 0 - 9
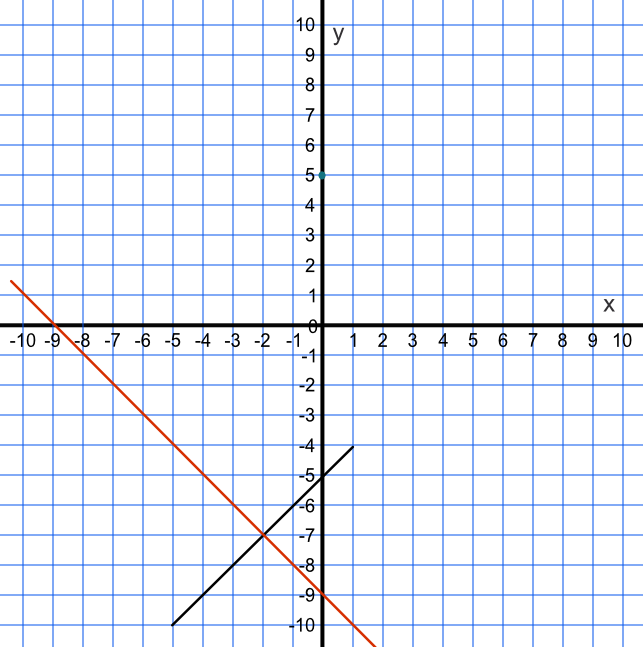
Answer: -9