An enlargement using a negative scale factor will cause the enlargement to appear on the other side of the centre of enlargement; and will be inverted (upside down). The shape will also change size depending on the value of the enlargement.
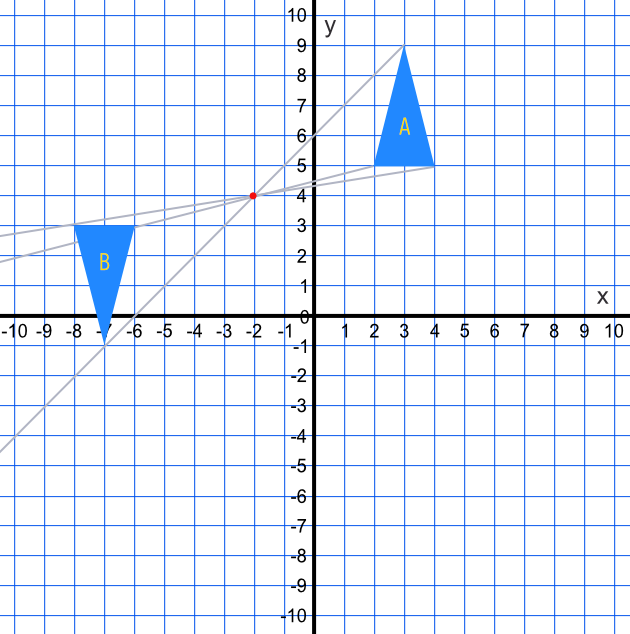
In the above example, shape A has been mapped onto shape B with a scale factor of -1. Note that the ray lines pass through centre of enlargement which inverts the shape.
Describe fully the transformation that maps shape A onto shape B.
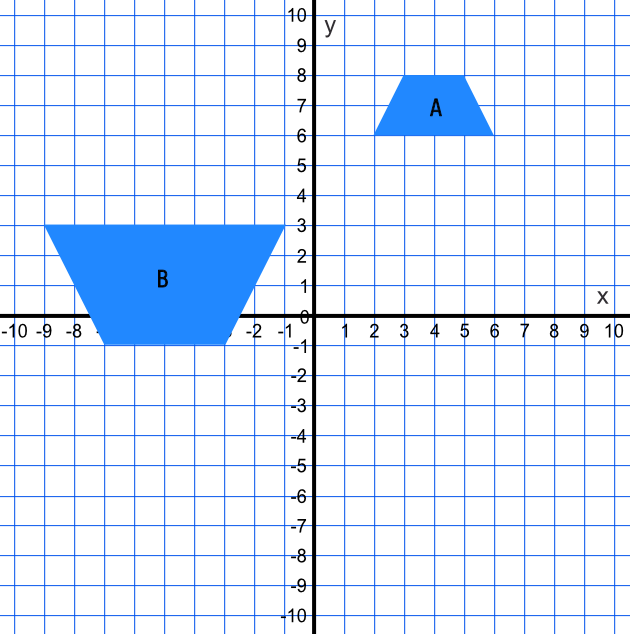
The shape has changed size, so it is an enlargement. It is inverted, so it has a negative scale factor.
Draw ray lines between the matching vertices. The ray lines cross at the centre of enlargement (1,5). The shape is twice the size of the original, scale factor 2; as it has been inverted and the enlargement is on the opposite side of the centre of enlargement the scale factor is -2.
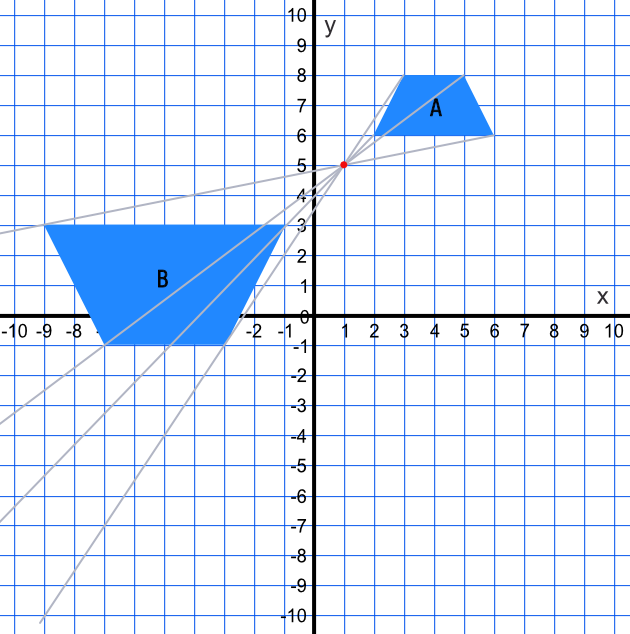
Answer: Enlargement, scale factor -2, centre of enlargement (1, 5)
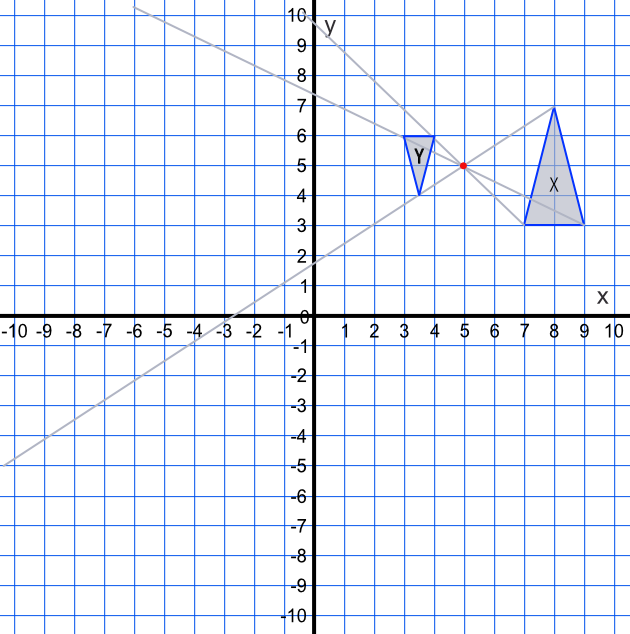
Shape X is mapped onto shape Y with a scale factor of -0.5, with a centre of enlargement at (5, 5). Show Shape Y.

Plot the position of the centre of enlargement (5, 5).
Draw ray lines from the vertices through the centre of enlargement.
Determine the distances, using the grid lines, from the vertices on shape X to the centre of enlargement. Halve these distances and determine the position of the vertices on the ray lines projected through the centre.
Check the enlargement by confirming that shape Y is half the size of shape X.
Answer: