A Reflection is a transformation.
A reflection requires a mirror line.
A mirror line reflects the original image. All the vertices, or corners, of the shape are always the same distance from the mirror line in the reflected image as they are in the original image.
Reflections may be shown on a grid, and the mirror line given as an equation.
To find a mirror line, locate the mid-point between each set of vertices, and draw the mirror line through these mid-points.
Describe fully the transformation that maps shape X onto shape Y.
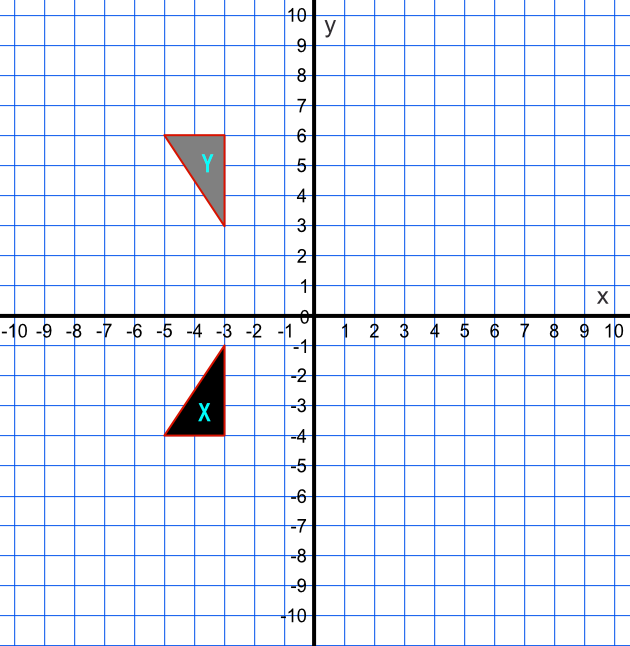
The vertical distance between the nearest points of the two images is 4 grid spaces; the mirror line lies halfway along that line. Repeat for the other vertices to determine the reflection line `y` = 1.
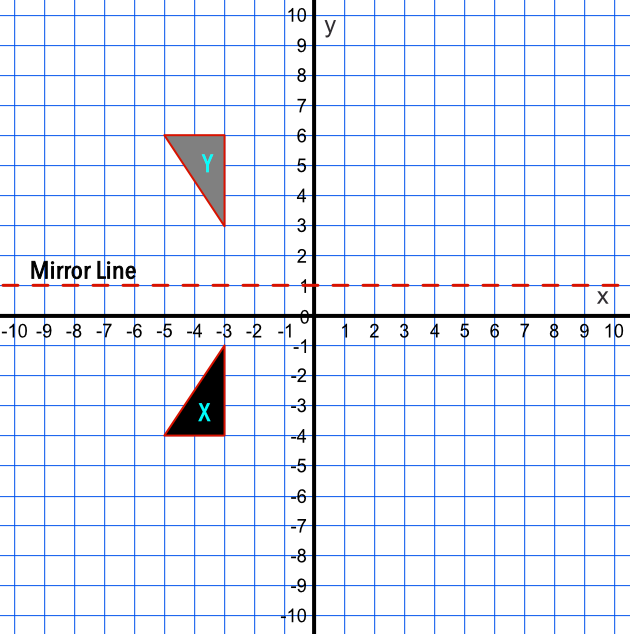
Answer: A reflection in the line `y` = 1
A shape X is reflected in the line `x` = -`y`. What is the position of the reflected shape: A, B, C or D?

Draw the mirror line on the graph.
Lines connecting the vertices of the original and the mirrored objects must be the same distance from the mirror line and must be at right angles to the mirror line.
Only shape C is valid.
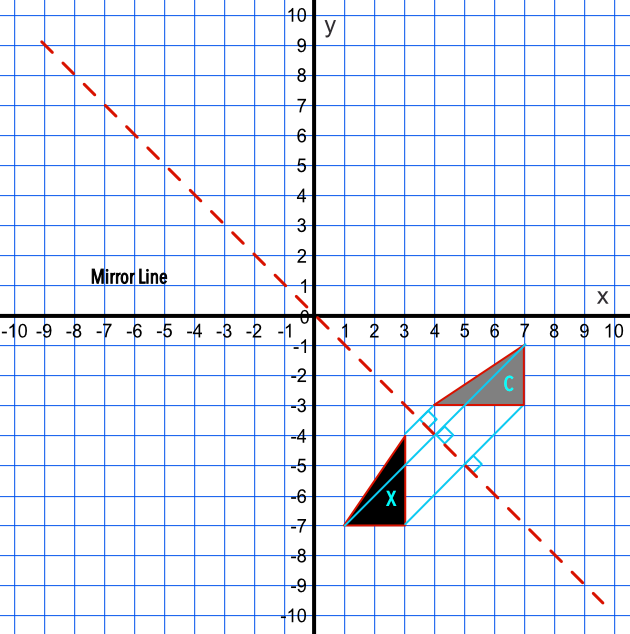
Answer: C