A ratio can be turned into a function. To turn a ratio into a function, one side of the ratio must be set to 1. A ratio of 3 : 7 can be turned into a ratio of 1 : `frac(7)(3)`.
With one side of the ratio set to 1, it can now be mapped as `x -> frac(7)(3)x`, or described as `f(x) = frac(7)(3)x`. The function can be drawn as a graph to show, for example, conversion rates between units (miles and kilometres) or currencies.
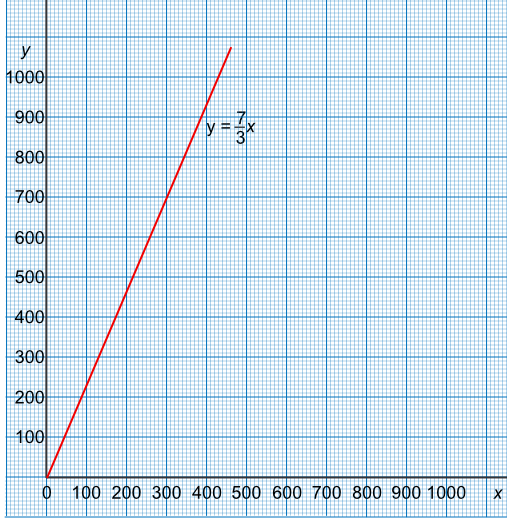
The gradient of the graph gives the ratio. The graph will also pass through (0,0).
A ratio 1:5 is mapped as a function, and plotted onto a graph. What is the gradient of the graph?.
The function will be plotted as `x -> 5x`. The gradient is given by `frac(text(up))(text(along))` = `frac(5)(1)`.
Answer: 5
A courier company charges a flat rate of £10, then £1.20 per kilometre. Can this be written as a ratio? Explain your answer.
If the charges were plotted as a graph against distance, the graph would not pass through the origin (0,0). This is not a ratio.
Answer: No. When one value of a ratio is zero, then all values of the ratio must be zero.