A line is drawn that is 5cm long. Applying a scale factor of 2, the line becomes 2 x 5cm = 10cm long.
A rectangle is drawn that is 5cm by 10 cm.
The area of the rectangle is `5 xx 10 = 50 text(cm)^2`.
Applying a linear scale factor of 2, the lengths of each side of the rectangle are doubled. The area of the rectangle becomes `10 xx 20 = 200 text(cm)^2`, which is four times larger.
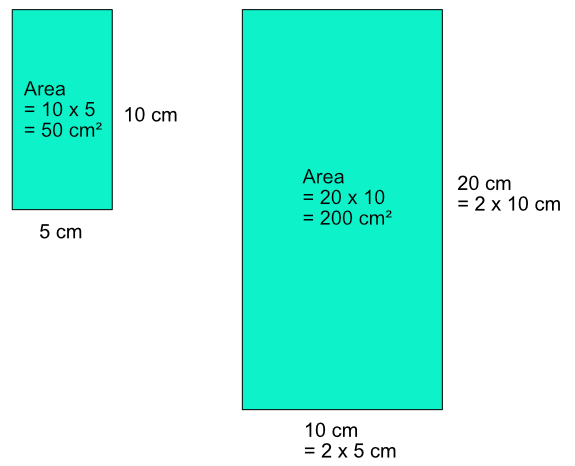
If a linear scale factor is applied to an area, then the area is increased by the square of the scale factor.
A cuboid is drawn that is `2 text(cm) xx 3 text(cm) xx 4 text(cm)`, which is a volume of 24cm3. Applying a linear scale factor of 2, the sides become `4 text(cm) xx 6 text(cm) xx 8 text(cm)`, giving a volume of 192cm3, which is 8 times larger.
If a linear scale factor is applied to a volume, then the volume is increased by the cube of the scale factor.
A cuboid has a volume of 22 cm3. A similar cuboid has a length that is 1.5 times the size of the original. What is the volume of the similar cuboid?
Give the answer to 1 decimal place.
The volume of a shape increases by a cube of the scale factor.
The volume of the enlarged cuboid is `22 xx 1.5^2 = 74.25`
To 1 dp this is 74.3cm3
Answer: 74.3 cm3
A rectangle, A, has an area of 100cm2. A similar shape, B, has an area of 200cm2. What is the scale factor to map A onto B? Give the answer correct to 2 decimal places.
A scale factor is squared when relating area
Rectangle A x scale factor2 = Rectangle B
Let `f` be the scale factor
| Write the relationship | A x `f^2` | `= B` |
| Substitute: | 100 x `f^2` | `= 200` |
| Divide both sides by 100 | `f^2` | `= 2` |
| Square root both sides | `f` | `= 1.412` |
| To 2dp | `f` | `= 1.41` |
Answer: 1.41