Solving an inequality means finding the values for which an inequality is true. Much of the process is similar to solving an equation: the solution is found by applying the same operations to both sides of the inequality to simplify the inequality.
Once the inequality has been simplified, select values to test in the original inequality to make sure that the solution is true.
One difference between solving equations and solving inequalities is when multiplying the inequality by a negative number. As well as changing the signs of the terms, you must also reverse the inequality sign.
An inequality that describes a range is solved in the same way: operations are applied to all three parts of the inequality until a single value of the variable is left.
Solve `6 - 4x ≥ 6(2 - x)` and show on a number line.
| `6-4x` | `≥` | `6(2- x)` | |
| Multiply out the brackets | `6- 4x` | `≥` | `12- 2x` |
| Subtract 6 from both sides | `- 4x` | `≥` | `6- 2x` |
| Add `6x` to both sides | `2x` | `≥` | `6` |
| Divide both sides by 2 | `x` | `≥` | `3` |
| Check for `x=3` should be true | 6 - 4(3) | ≥ | 6(2 - (3)) |
| = -6 ≥ -6 true ✔ | |||
| Check below (`x=0`) should be false | 6 - 4(0) | ≥ | 6(2 - (0)) |
| = 6 ≥ 12 false ✔ | |||
| Check above (`x=5`) should be true | 6 - 4(5) | ≥ | 6(2 - (5)) |
| = -14 ≥ -18 true ✔ |
Answer:
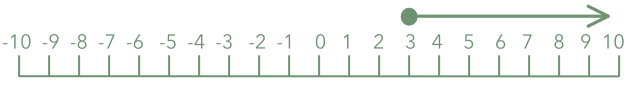
Which integers satisfy `9 < 2x + 3 < 19`?
| `9` | `<` | `2x+ 3` | `<` | `19` | ||
| Subtract 3 from each part | `6` | `<` | `2x` | `<` | `16` | |
| Divide each part by 2 | `3` | `<` | `x` | `<` | `8` | |
| Integers that satisfy: | `4,` | `5,` | `6,` | `7` | `` | `` |
| Check for `x=4` should be true | 9 < 2(4) + 3 < 19 |
| = 9 < 11 < 19 true ✔ | |
| Check for `x=7` should be true | 9 < 2(7) + 3 < 19 |
| = 9 < 17 < 19 true ✔ | |
| Check below (3) should be false | 9 < 2(3) + 3 < 19 |
| 9 < 9 < 19 false ✔ | |
| Check above (8) should be false | 9 < 2(8) + 3 < 19 |
| = 9 < 19 < 19 false ✔ |
Answer: 4, 5, 6 and 7
See also Solving Linear Equations