The formula for the surface area of a pyramid is based on three items: the length of the slope on each face; the area of each face; and the area of the base.
The slope length of each face is calculated using Pythagoras` Theorem: the slope length for one face is
`s = sqrt(h^2 + (frac(1)(2)l)^2)`
and similarly for the other three faces. Note that the base of the triangle is either `frac(1)(2)l` or `frac(1)(2)w`.
If the pyramid is based on a square or rectangle then congruent faces will have the same slope length.
From the sloping length, calculate the area of each triangular face:
`text(Area) = frac(1)(2)ws` or `text(Area) = frac(1)(2)wl`
Finally calculate the area of the base `text(Area) = lw`.
Add the areas for the four parts together.
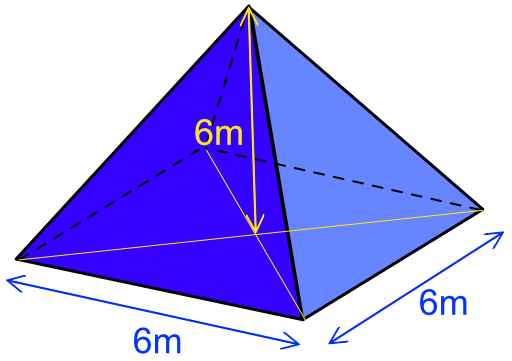
A structure has been built in the shape of a right square pyramid. The vertical height is 6m, and the length of each side is 6m at its base. To the nearest whole metre, what is the surface area off the entire structure?
| Centre to side (b) | b | `= frac(1)(2) xx 6` |
| `= 3` | ||
| Slope length (c) | c | `= sqrt(a^2 + b^2)` |
| `= sqrt(6^2 + 3^2)` | ||
| `= 6.708` | ||
| Area of face | Aface | `= frac(1)(2)(6)(6.708)` |
| `= 20.125` | ||
| Area of base | Abase | `= wl` |
| `= (6)(6)` | ||
| `= 36` | ||
| Total Area | A | = 4Aface + Abase |
| `= 4(20.125) + 36` | ||
| `= 116.498` |
Answer: 116 m2
A shape for an engineering component has been manufactured as a pyramid.
What is the surface area of the sloping sides of the pyramid, which has a base of 9cm by 6cm and a vertical height of 4cm?
Give your answer to 1 decimal place.
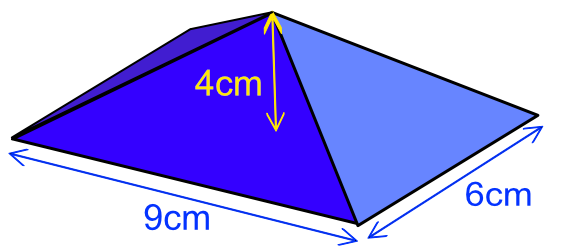
The sloping areas consist of two sets of two triangles.
The lengths from the centre of the base to the edge are 3cm and 4.5cm.
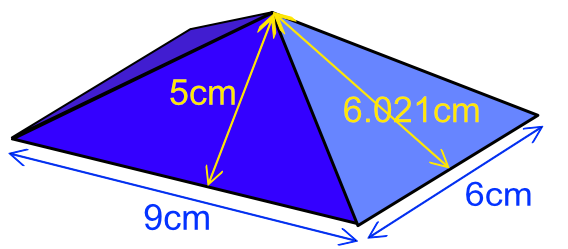
| Slope lengths | s1 | `= sqrt(3^2 + 4^2)` |
| `= 5` | s2 | `= sqrt(4.5^2 + 4^2)` |
| `= 6.021` |
| Area of Sides | A1 | `= frac(1)(2)(9)(5)` |
| `= 22.5` | ||
| A2 | `= frac(1)(2)(6.021)(6)` | |
| `= 18.063` | ||
| TOTAL | Area | `= 2A_1 + 2_A2` |
| TOTAL | Area | `= 2(22.5) + 2(18.063)` |
| `= 81.126` |
Answer: 81.1 cm2