The ratio of the opposite side to the adjacent is the tangent, or tan of the angle.
For tan questions, the hypotenuse is not used.
The adjacent side is the side that touches the angle: the opposite side is opposite the angle.
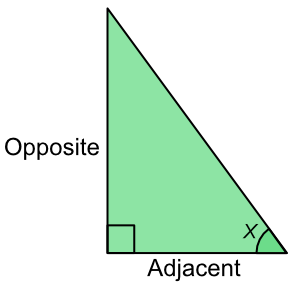
`tan x = frac(text(Opposite))(text(Adjacent))`
This is the TOA part of SOH CAH TOA, and is taken from the formula above.
If an angle and one length is known, find the tan of the angle and substitute this value into the formula along with the known length. Use the tan key on your calculator to get the tan value for the angle.
If the lengths are known, but not the angle, then the formula gives the tangent of the angle. Use the tan-1 key on your calculator to get the value of the angle.
The tan key on your calculator changes the angle to the tan value of the angle.
The tan-1 key on your calculator is the inverse and changes the tan value to the value of the angle itself.
What is the length of BC? Give the answer to 2 decimal places.
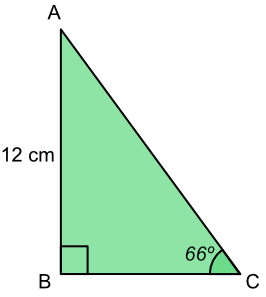
| TOA | `Tan (x)` | `=frac(text(Opposite))(text(Adjacent))` |
| substitute | `tan (66)` | `=frac(12)(text(BC))` |
| `2.246` | `=frac(12)(text(BC))` | |
| multiply both by BC | `2.246 x BC` | `=12` |
| ÷2.246 both sides | `BC` | `= 12 ÷ 2.246` |
| `BC` | `= 5.342` | |
| to 2dp | `BC` | `= 5.34` |
Answer: 5.34 cm
What is the value of the angle `x`? Give your answer to the nearest degree.
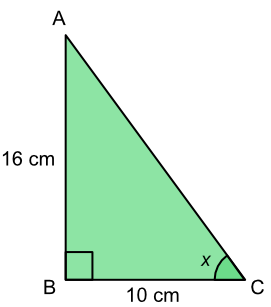
| TOA | `Tan (x)` | `=frac(text(Opposite))(text(Adjacent))` |
| substitute | `tan (x)` | `=frac(16)(10)` |
| `=1.6` | ||
| tan-1 both sides | `x` | `=tan^-1 (1.6)` |
| `= 57.995º` | ||
| to degree | `= 58º` |
Answer: 58º