Most trigonometry problems in three dimensions will involve Pythagoras.
Solving the problems involve analysing individual planes, or flat surfaces, to build up a 3D answer. The isometric view in the diagram below distorts the angles of the triangles. Note that ABD is a right angle, and that ADH is also a right angle.
The diagonal AH in the diagram below crosses the cube from bottom left to top right on opposite corners.
ADH is a right-angled triangle (the right angle is at D).
To work out AH, you need to know AD and DH. DH is the height. And AD is the hypotenuse of the triangle ABD.
AB and BD are both known, so AD can be calculated.
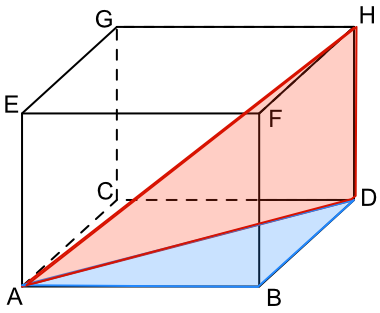
In most instances with 3D Pythagoras problems, it is necessary to find two right angled triangles with the hypotenuse for one being a shorter side for another.
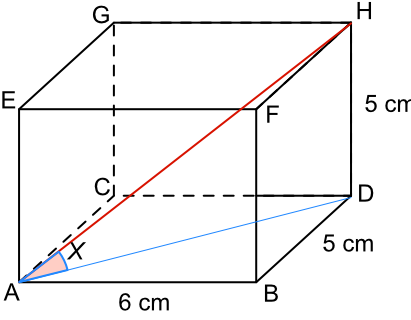
What is the length of the diagonal, AH, in this cuboid?
| Work out AD using AB and BD | `a^2 + b^2` | `= c^2` |
| Substitute | `(6)^2 + (5)^2` | `= c^2` |
| `61` | `= c^2` | |
| root both sides | `7.810` | `= c` |
| c is AD | ||
| Work out AH using AD and DH | `a^2 + b^2` | `= c^2` |
| Substitute | `(7.810)^2 + (5)^2` | `= c^2` |
| `86` | `= c^2` | |
| root both sides | `9.274` | `= c` |
Note that `(AH)^2 = (AB)^2 + (BD)^2 + (DH)^2`
Answer: 9.274 cm
Using the cuboid, above, determine the size of the angle X that the diagonal AH makes with the bottom plane of the box ABCD.
Give the answer to the nearest degree.
All three side lengths known, use any method from SOH CAH TOA
| sin = `frac(text(opposite))(text(hypotenuse))` | sin(`x`) | `= frac(5)(7.81)` |
| `= 0.640` | ||
| sin-1 both sides | `x` | `= sin^-1(0.640)` |
| `= 39.807º` | ||
| to nearest degree | `= 40º` |
Answer: 40º