Density is the mass of a substance that occupies a given volume.
`text(density) = frac(text(mass))(text(volume))`, or `D = frac(M)(V)`
Density is normally measured using units of g/cm3 for smaller amounts, and kg/m3 for larger amounts.
Calculations of density can be represented by a triangle:
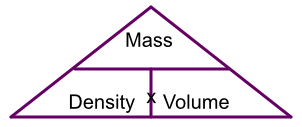
To work out the mass, cover up mass on the triangle and you see density x volume. To work out density, cover up density and you see mass over volume, and for volume it is mass over density.
Pressure is a force acting on an area. A force pressing down on a point will exert more pressure than the same force acting over a wide area. Force is measured in Newtons (shown as N) and the area is normally given in square metres.
`text(pressure) = frac(text(force))(text(area))`, or `P = frac(F)(A)` and is shown as N/m2, or Nm-2
The formula can also be represented by a triangle:
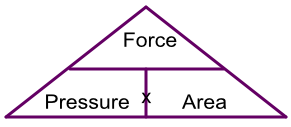
A pair of stiletto heels occupy an area of 2cm2. What is the pressure being applied to a floor if the weight of the woman wearing the stilettos is 560N?
Unknown is the pressure: using the triangle gives Force ÷ Area = 560 ÷ 2 = 280 N/cm2
Answer: 280 N/cm2
4 grams of gold occupy 0.207cm3. What is the density of gold?
Hiding density on the triangle gives mass over volume. 4 ÷ 0.207 = 19.3 g/cm3 to 1 dp.
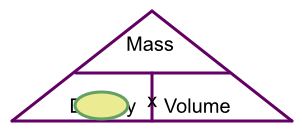
Answer: 19.3 g/cm3
See also Compound Units