A linear function - such as a straight line on a graph - has a constant rate of change. As `x` changes, so does `y`, and this is constant. The rate of change can be derived from the gradient:
`frac(text(change in )y)(text(change in )x)`.
For other functions, the rate of change varies over the function: in other words, the gradient on a graph becomes steeper or flatter. At any one point on the graph, the rate of change can be derived (by drawing a tangent to the graph at that point). At a different point, a different rate of change can be found by obtaining the gradient at that point.
A car covers a distance of 20m in 5s. If the car has a constant rate of acceleration, what is the increase in the velocity of the car beween 5s and 10s?
The kinematic formulae are:
`v = u + at, s=ut+frac(1)(2)at^2` and `v^2=u^2+2as`
where `u` is initial velocity, `v` is final velocity, `s` is distance, `a` is acceleration and `t` is time.
Known values: `s=20, t=5, u=0`
| Work out the acceleration | `s` | `=` | `ut + frac(1)(2)at^2` |
| `(20)` | `=` | `(0)(5) + frac(1)(2)a(5)^2` | |
| `a` | `=` | `frac(8)(5)` | |
| Velocity at 5s | `v` | `=` | `u + at` |
| `v` | `=` | `(0) + frac(8)(5)(5)` | |
| `v` | `=` | `8` | |
| Velocity at 10s | `v` | `=` | `u + at` |
| `v` | `=` | `(0) + frac(8)(5)(10)` | |
| `v` | `=` | `16` |
Difference in velocity = 16 - 8 = 8ms-1
Answer: 8 ms-1
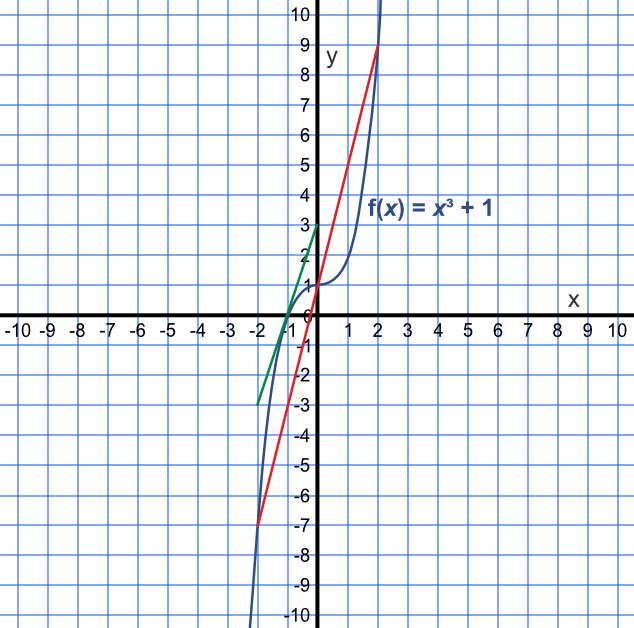
The gradient of `x^3+1` is the same at (-2, -7) as it is at (2, 9). The gradient at (0, 1) is zero.
Jon draws line from (-2, -7) to (2, 9) which passes through (0, 1). Jon states that the rate of change between (-2, -7) and (2, 9) is constant as his line also passes through (0, 1).
Why is Jon wrong?
Draw a tangent at (-1, 0) (or some other point) to find a different gradient.
Answer:
Jon has drawn the average rate of change between these two points.
The rate of change is constantly varying eg it is zero at (0, 3) and 3 at (-1, 0).