Venn Diagrams

Venn Diagrams are used to display sets. A Venn diagram consists of one or more circles within a rectangle.

The rectangle defines the Universal Set, and each circle within the rectangle is a different set. Elements not in any set are shown within the rectangle but not inside a circle.

For example, if two dice are thrown then ε = {2,3,4,5,6,7,8,9,10,11,12). Set P consists of Prime Numbers and set Q consists of odd numbers:

Venn diagram intersection of two sets of numbers

Venn Diagrams can be used to determine the interaction of sets. The areas of white in the diagrams below show the result of the operation:

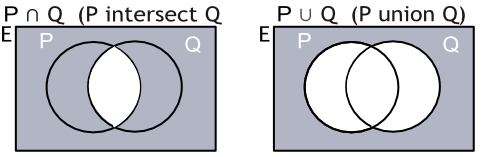
Venn diagrams showing 1) intersect and 2) union

`P nn Q = {3, 5, 7, 11}` and `P uu Q = {2, 3, 5, 7, 9, 11}`.

Venn diagrams can also be used to show totals, rather than individual items.

Example 1

Given a set of integers from 1 to 15, set A = {multiples of two} and set B = {multiples of three}. The Venn Diagram has been started. Show the elements of A ∩ B.

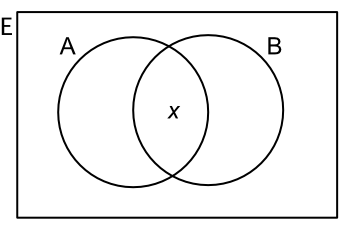
Venn Diagram showing x as unkown in intersect

`A={2,4,6,8,10,12,14}` and `B={3,6,9,12,15}`

Part x is A overlapping B, which is `A nn B = {6, 12}`.

Answer: `A nn B = {6, 12}`

Example 2

A field trip consists of 30 students. 8 of these students do not study a language.

21 students study French. 18 students study German. Complete the Venn Diagram, finding values for w, x, y and z.

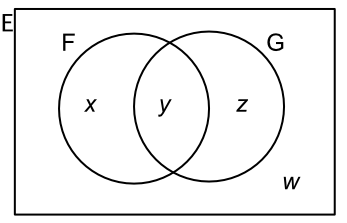
Venn diagrams showing unknowns in three areas

The 8 students that do not form part of any set are shown outside the sets in position w.

The total for French and German is 21 + 18 = 39, but there are only 22 students that study a language. The number of students studying two languages is 39 - 22 = 17 = y.

There are 21 students studying French less the 17 studying both = 4 = x.

Similarly for German: 18 - 17 = 1 = z.

Check it: w + x + y + z = 30✔

Answer: w = 8, x = 4, y = 17, z = 1