The formula for a right rectangular pyramid is:
`V = frac(lwh)(3)`
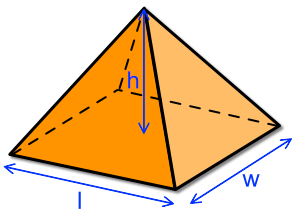
A right rectangular pyramid is a pyramid that has a rectangle as a base. The right part of the definition comes from the fact that a triangle formed by the height, a sloping slide and the distance from the centre of the rectangle to the sloping side is a right angle.
Also note that the `h` is the height of the triangle.
A right rectangular pyramid is based on a square, and the vertical height is the same value as the sides of the square.
If the volume of the pyramid is 72 cm3, what is the area of the base of the pyramid?
Let `h, l, w = x` as they are all the same value
| Pyramid: | `V` | `= frac(1)(3) hlw` |
| Substituting | `72` | `= frac(1)(3) x^3` |
| `216` | `= x^3` | |
| `x` | `= 6` | |
| Area of base | `A` | `= x^2` |
| `= 36` |
Answer: 36 cm2
Two right rectangular pyramids are being compared. Both pyramids have a square base. One pyramid has twice the vertical height of the other. The lower pyramid has twice the base area of the higher pyramid.
Do both pyramids have the same volume?
Let the smaller height be `x`
Let the smaller area be `y`
Volume (taller) = `frac(1)(3) xx 2x xx y`
Volume (shorter) = `frac(1)(3) xx x xx 2y`
`frac(1)(3) xx 2x xx y = frac(1)(3) xx x xx 2y`
Simplifying, 2 = 2
Answer: Yes