The gradient of a graph showing velocity against time is the acceleration:

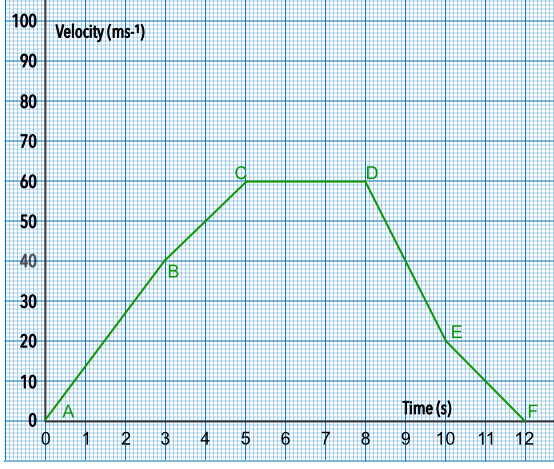
In the first part of the graph (AB), the object is accelerating at a constant rate (and, therefore, the object is moving faster and faster). In the second part of the graph (BC), the object is still accelerating but as the gradient is slightly lower then the increase in velocity is not as rapid.

acceleration = `frac(text(velocity))(text(time))`

BC shows a gradient of zero: the velocity remains constant. The gradient in sections DE and EF are negative, and indicate that the object is braking.

On a velocity-time graph, the area under the graph gives the distance travelled.