Parallel lines are shown on diagrams with an arrow. If there is more than one set of parallel lines, then the arrows are doubled up.
When a line crosses a pair of parallel lines, it creates two sets of angles. Each set of angles has the same value and adds to 360º. Note that each adjacent pair of angles (125º and 55º) add up to 180º because they are a straight line.

Angles which are within the parallel lines, but on opposite (or alternate) sides of the single line, are alternate Angle:
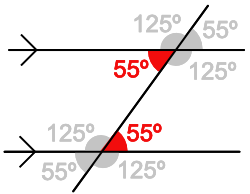
Note that, in the above diagram, the pair of 125º angles are also alternate angles.
Angles which appear on the same place on each of the parallel lines are called corresponding angles:

In the above diagram, there are other pairs of corresponding angles.
What is the size of the angle marked A?
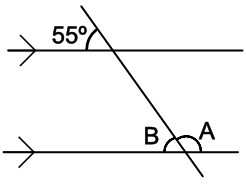
The angle B and the angle 55º are corresponding angles, so B = 55º.
The angles B and A add to 180º (straight line). Angle A is 180 - 55 = 125º
Answer: 125º
What is the size of the angle marked A?
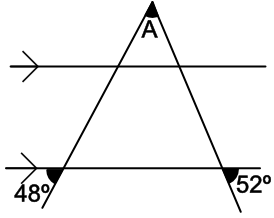
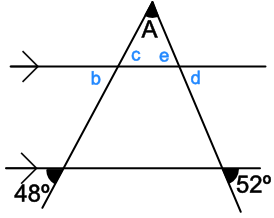
Angle b is a corresponding angle to 48º and is therefore 48º.
The angle opposite that (angle c) is also 48º.
Similarly, angle d is a corresponding angle to 52º and is therefore also 52º. Angle e is also 52º as it is opposite d.
The angles A, c and e make a triangle; a triangle has angles that add up to 180º. 180 - 48 - 52 = 80º
Answer: 80º