An angle between the tangent and the chord is therefore equal to the angle in the alternate segment.
The alternate angle is the angle made in the other sector from a chord. In the example below, the alternate angle to ∠ACD (shown as `x`) is the angle ∠ABC - it is on the other side of the chord.
Note: you do not need to know how to prove this, but you do need to know the theorem and how to use it.
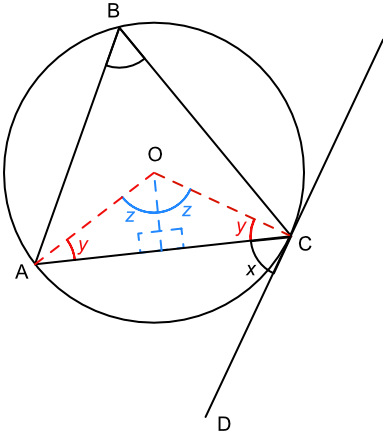
DC is a tangent to the circle. A triangle ∠ABC has points A, B and C on the circumference of a circle with centre O.
Let the angle ∠ACD be `x`. Add a triangle AOC with the angle ∠OCA as y.
A tangent is at right angles to the radius; therefore `x + y = 90º`
Bisect the triangle ∠AOC from the centre: the triangle is an Isosceles triangle and the bisecting line meets the chord at a right angle. Let the bisected angle have a value of `z`.
Angles in a triangle add to 180º; `z + y + 90 = 180`, or `z + y = 90º`.
Match the two equations: `x + y = z + y` therefore `x = z`
The angle at the centre is twice the value of the angle at the circumference when subtended by the same arc: ∠AOC = 2`z` therefore ∠ABC = z = x.
ED is a tangent to a circle, touching at point A. Triangle ABC is a triangle proscribed within the circle. Angle ∠DAC has a value of 59º. What is the value of angle ∠ABC?
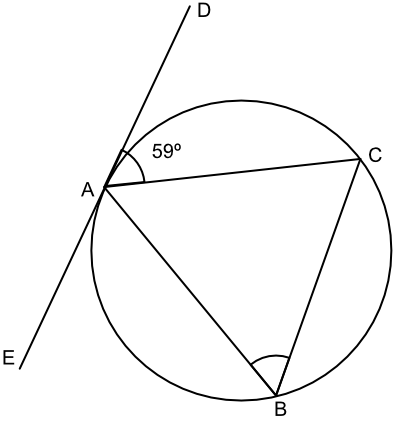
Alternate Segment: the angle between the tangent and the chord is equal to the value of the angle in the alternate segment.
Answer: 59º
What is the value of the angle ∠DAC, when DA is a tangent to a circle and ABC is a triangle with points on the circumference of the circle?
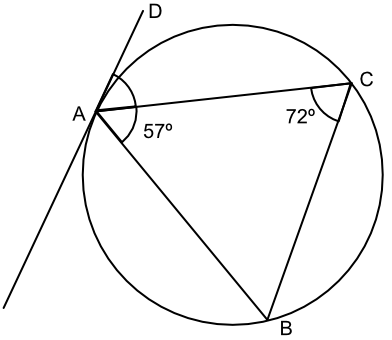
Angles in a triangle add to 180º: ∠ABC = 180 - 57 - 72 = 51º
The angle between a tangent and the chord is equal to the angle in the alternate segment.
Answer: 51º
See also Circle Theorems - Subtended Angles