The angle at the centre of a circle is twice the angle at the circumference when both are subtended by the same arc.
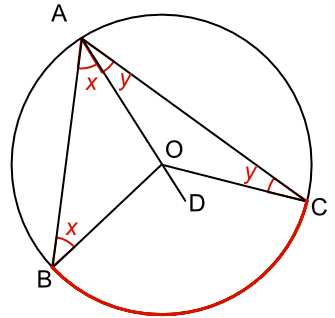
Proof: an arc BC is drawn on the circumference of a circle. Draw a line from these points to the centre of the circle (lines BO and CO). Draw also a line from these points to a point on the circumference (lines BA and CA).
A line from point A is extended through the centre to point D to create two triangles.
Angle ∠BAO = angle ∠ABO = `x` (AO, BO and CO are radii; both triangles are isosceles).
The value of angle ∠BOD = 2`x` (∠AOB = 180 - 2x; and ∠BOD = 180 - (180 - ∠AOB))
Similarly for the other triangle, ∠COD = 2`y`
Angle ∠BAC = `x` + y
Angle ∠BOC = 2`x` + 2`y` = 2(`x` + `y`)
Therefore the angle at the centre of a circle is twice the angles at the circumference when subtended by the same arc.
What is the size of the angle ∠BOC?
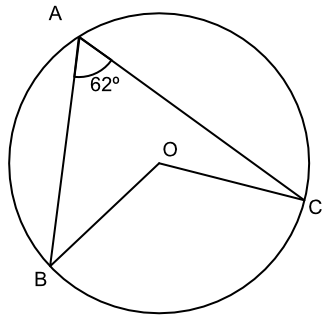
The angle is twice the size of the angle ∠BAC (angle at the centre of a circle is twice the angle at the circumference when subtended by the same arc).
Answer: 124º
What is the size of the angle ∠BAC?
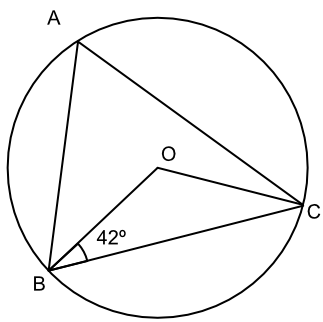
Triangle BOC is an isosceles triangle (OB and OC are radii); therefore angle ∠OCB = 42º.
Angle ∠BOC = 180 - 42 - 42 = 96º
Angle subtended at the centre is twice the angle subtended at the circumference when on the same arc: 96 ÷ 2 = 48º
Answer: 48º