Circle Theorems - Semicircle

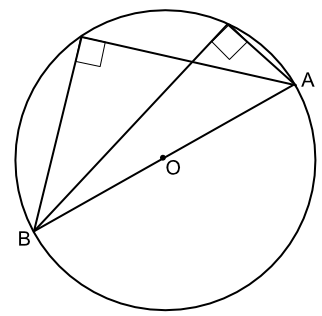
The angle at the centre of a circle is twice the angle at the circumference when subtended by the same arc: consider a case where the arc covers 180º.

The angle at the centre of the circle is 180º. The angle at the circumference is therefore 90º, as the angle subtended at the centre is twice the angle subtended at the circumference.

Circle theory: angle at circumference is 90 degrees

Example 1

Points A, B and C are on the circumference of a circle with centre O. Angle ∠ABC has a value of 19º. What is the value of the angle ∠ACB?

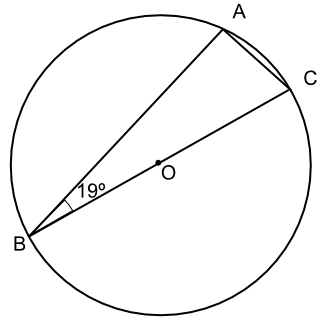
Circle theory: what is angle given the chord is a diameter

For a semicircle, the angle at a circumference is 90º. Angle A is 90º.

The angles in a triangle add up to 180º.

Therefore 180 - 90 - 19 = 71º.

Answer: 71º

Example 2

What is the value of x in the diagram below?

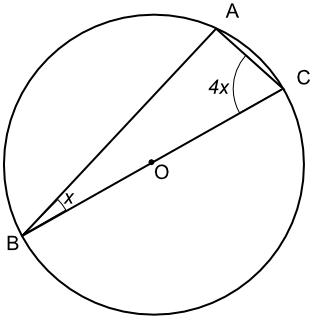
Circle theory: calculate value of x when chord is a diameter

For a semicircle, the angle at a circumference is 90º.

180	= 90 + x + 5x
90	= 5x
18	= x

Answer: 18º

Next: Circle Theorems - Segment Angles