Circle Theorems - Tangents

A tangent is a line that just touches the circumference of a circle. It can touch at any point on the circumference. At the point of contact, the angle between the tangent and the radius is 90º.

Circle theory: tangent is a right angle to a radius

In the diagram below, AC and BC are both tangents to a circle. Triangles OAC and BOC are congruent (identical): OC is common to both triangles, and in each case opposite a right angle; and OA and OB are both equal lengths (radius). As the triangles are congruent, AC = BC.

Tangents to a circle drawn to a point outside the circle are equal in length.

Circle theory: tangents to a point are equal lengths

Example 1

Give the size of the angle ∠ACB.

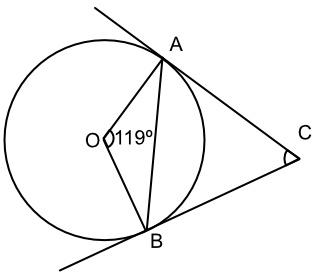
Circle theory: question using tangent angles

∠OAC is a right angle; as is ∠OBC.

Angles in a quadrilateral add up to 360º

360 - 90 - 90 - 119 = 61

Answer: 61º

Example 2

A, B and D are points on the circumference of a circle with a centre O. AC and BC are tangents to the circle. ∠ACB has an angle of 61º. What is the size of ∠ADB?

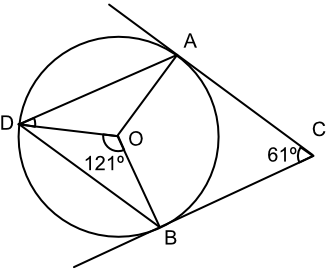
Circle theory: question using tangents

Angles in a quadrilateral = 360º and ∠OAC and ∠OBC are right angles

∠AOB = 360 - 90 - 90 - 61 = 119º

AOB and ADB are subtended angles on the same chord.

∠ADB = `frac(1)(2)` ∠AOB

∠ADB = `frac(119)(2)` = 59.5º

Answer: 30º