A Conditional Probability Tree is used to determine the change in probabilities as events take place when events depend upon the outcome of earlier events.
For example, if items are taken from a container and not replaced, then the number of items in the container goes down by one. In fraction terms, this changes the denominator. The numerator may also change, depending on what was selected the first time.
Such probabilities re best tackled using a probability tree.
A box of chocolates consists of either milk chocolates or plain chocolates. There are 12 milk chocolates and 8 plain chocolates. A chocolate is taken and eaten. A second chocolate is taken. What is the probability that both chocolates were plain?
The probability of drawing a plain chocolate the first time is `frac(8)(20)`. The probability of drawing a plain chocolate again changes to `frac(7)(19)`, as there is one fewer plain chocolates to select, and 19 fewer chocolates in total.
Multiply the two probabilities together to obtain the probability of drawing two consecutive plain chocolates:
`frac(8)(20)` x `frac(7)(19)` = `frac(56)(380)` = `frac(14)(95)` (multiply along the branches).
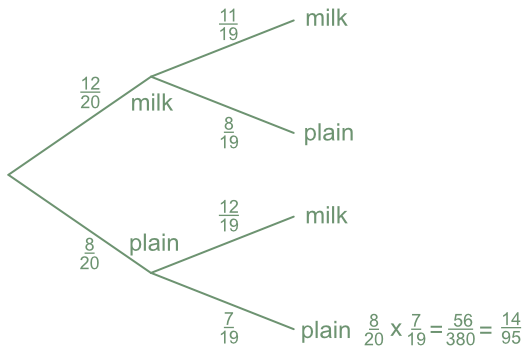
Answer: P(both plain) = `frac(14)(95)`
For the box of chocolates indicated above, what is the probability of eating two different types of chocolate?
The two possibilities are milk then plain; or plain then milk.
For the first possibility, there are initially 12 milk out of 20 = `frac(12)(20)`. The next chocolate is plain: there are 8 plain chocolates left out of a total of 19 chocolates = `frac(8)(19)`.
P(milk-plain) = `frac(12)(20)` x `frac(8)(19)` = `frac(96)(380)`
P(plain-milk) = `frac(8)(20)` x `frac(12)(19)` = `frac(96)(380)`
P(milk-plain) + P(plain-milk) = `frac(96)(380)` + `frac(96)(380)` = `frac(48)(95)`
(When working vertically on a tree diagram, add the totals at the end of the branches).
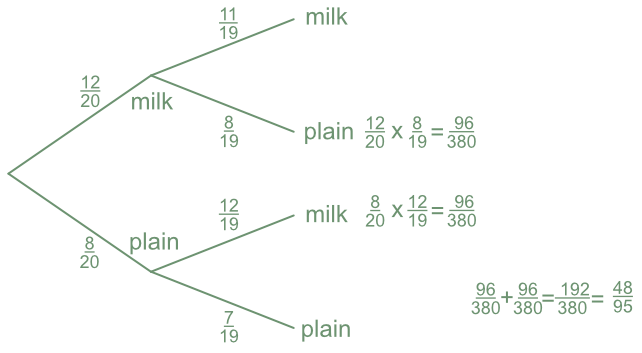
Answer: P(different) = `frac(48)(95)`