Cosine Rule

The cosine rule can be used for any triangle. The letters relating to the side are opposite the corresponding letters for the angles, i.e. a and A; b and B and c and C.

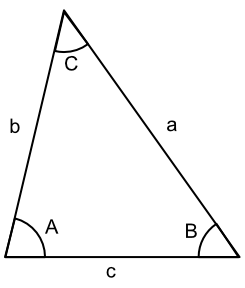
Cosine rule: angle and side naming convention

The rule is:

`a^2 = b^2 + c^2 - 2bc cosA`

Use the cosine rule when all three sides are known, or two sides and an included angle are known. Make sure that the length on the left hand side of the formula (a) is opposite the angle stated on the right hand side of the formula (cos A).

Example 1

What is the length of BC? Give your answer to 2 decimal places.

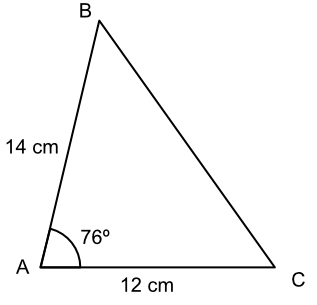
Cosine rule: calculating a missing length

Two sides and an included angle given, use the Cosine rule.

COSINE rule:	`a^2`	`= b^2 + c^2 - 2bc cosA`
substitute	`a^2`	`= (12)^2 + (14)^2 - 2(12)(14) cos(76)`
	`a^2`	`= 144 + 196 - 336 xx 0.24192`
	`a^2`	`= 258.71488`
	`a`	`= 16.0846`
to 2dp	`a`	`= 16.08`

Answer: 16.08 cm

Example 2

What is the size of the angle `x`? Give your answer to 1 decimal place.

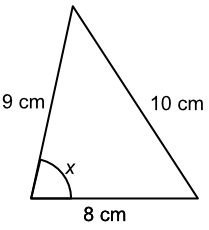
Cosing rule: calculating a missing angle

Three sides given; use the cosine rule:

COSINE rule:	`a^2`	`= b^2 + c^2 - 2bc cosA`
substitute	`(10)^2`	`= (8)^2 + (9)^2 - 2(8)(9) cosA`
	`100`	`= 155 - 144 cosA`
	`-55`	`= -144 cosA`
	`0.3819`	`= cosA`
cos^-1 both sides	`67.546`	`= A`
to 1dp	`67.6`	`= A`

Answer: 67.5º