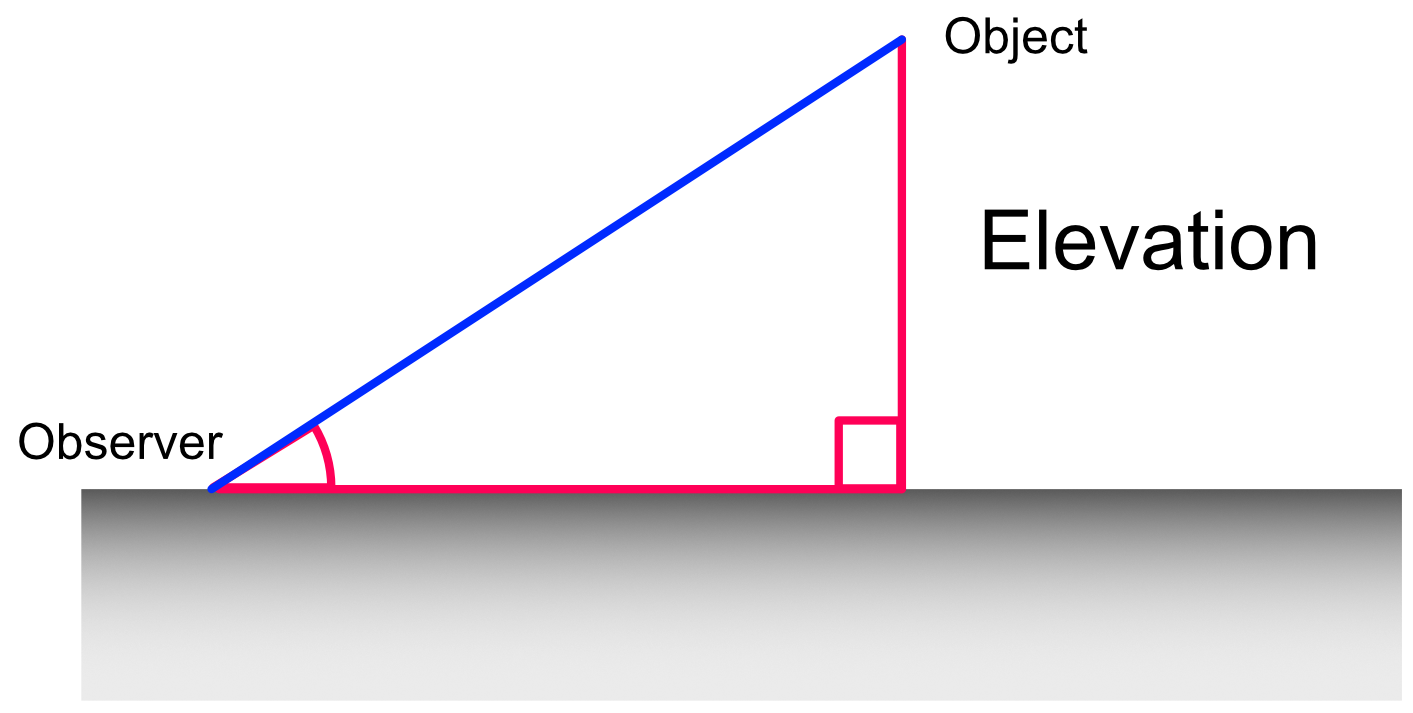
Elevation is the value, in degrees, that an object is above the observer. Create a triangle using the distance from the observer to the object, the height of the object above the ground, and the horizontal distance from the observer to the object.
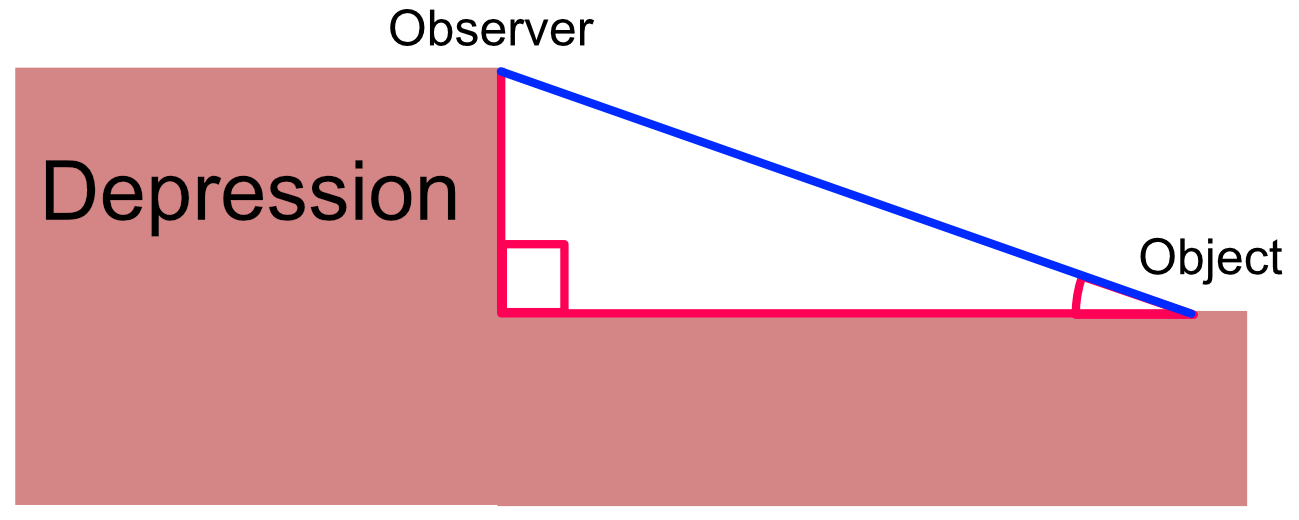
Depression is the value in degrees that a value is below the observer. Establish a triangle in the same way as for an elevation.
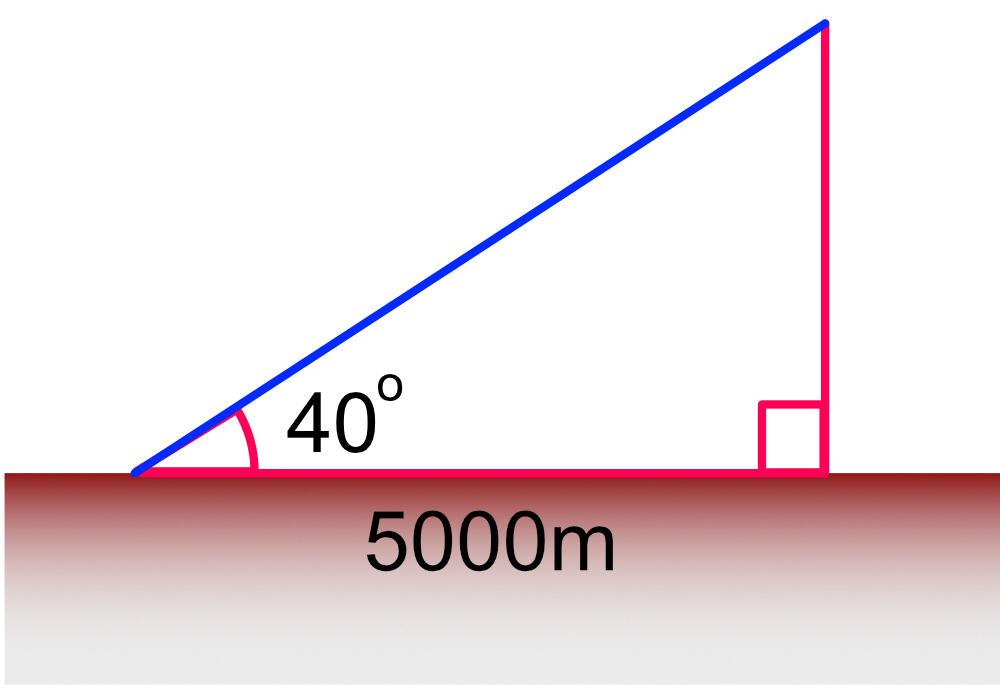
An aircraft is flying above a building, which is known to be 5000m away. The elevation of the aircraft is 40º. How high is the aircraft above the building, to the nearest metre? Ignore the height of the building and the height of the observer.
The height is opposite the angle of elevation. The angle and adjacent side are known.
Use TOA from SOH CAH TOA
| TOA | `tan x` | `= frac(text(opposite))(text(adjacent))` |
| substitute | `tan (40)` | `= frac(h)(5000)` |
| `0.839 x 5000` | `= h` | |
| `4195.498` | `= h` | |
| nearest metre | `4195` | `= h` |
Answer: 4195 m
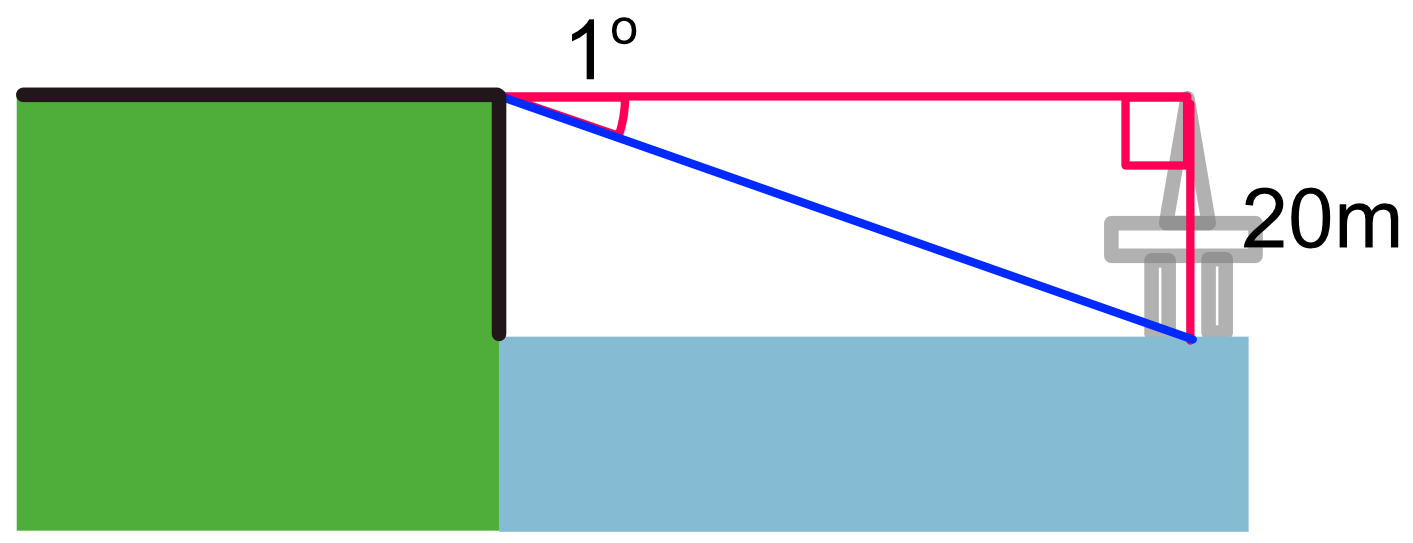
From a clifftop, an observer can see an oil rig. The top of the oil rig is level with the top of the cliff. The top of the oil rig is 20m above the sea. From the clifftop, the depression from the top of the oil rig to sea level is 28º. To the nearest metre, how far away is the oil rig from the clifftop?
Use SOH CAH TOA. The angle and opposite side are known.
| TOA | `tan x` | `= frac(text(opposite))(text(adjacent))` |
| substitute | `tan (1)` | `= frac(20)(x)` |
| `x` | `= frac(20)(tan (1))` | |
| `x` | `= frac(20)(0.0175)` | |
| `x` | `= 1142.86` | |
| nearest m | `x` | `= 1143` |
Answer: 1143m