An Enlargement is the only transformation that changes the size of a shape.
Two items of information are required to enlarge a shape: the Centre of Enlargement and the Scale Factor.
Locate the Centre of Enlargement, then draw Ray Lines from the centre of enlargement through the vertices of the shape.
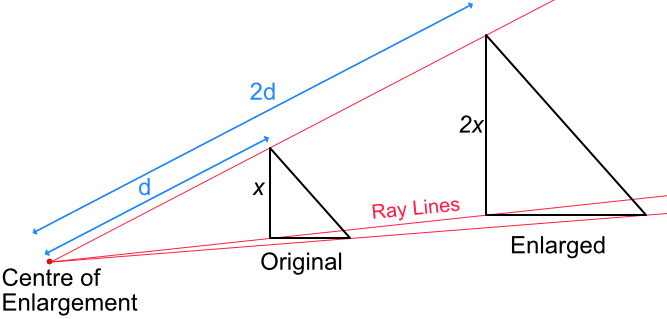
If a shape is being enlarged by a scale factor of 2, the distance from the centre of enlargement to each vertex will be twice the size. The size of the shape will also be twice the size.
Enlargements will preserve the angles of the shape.
Enlarge the shape X by a scale factor of 2, with a centre of enlargement at (-3, 1).

One vertex of the triangle is at (2, 2). This is 5 along from the centre of enlargement; and 1 up. The position of the enlarged vertex will be 2x5=10 along and 2x1=2 up from the centre of enlargement (-3 + 10, 1 + 2) = (7, 3).
Similarly, calculate the other two vertices. Draw ray lines for both triangles and check that the ray lines go through the Centre of Enlargement.
Check also that the new shape is twice as large as the original shape.
Answer:
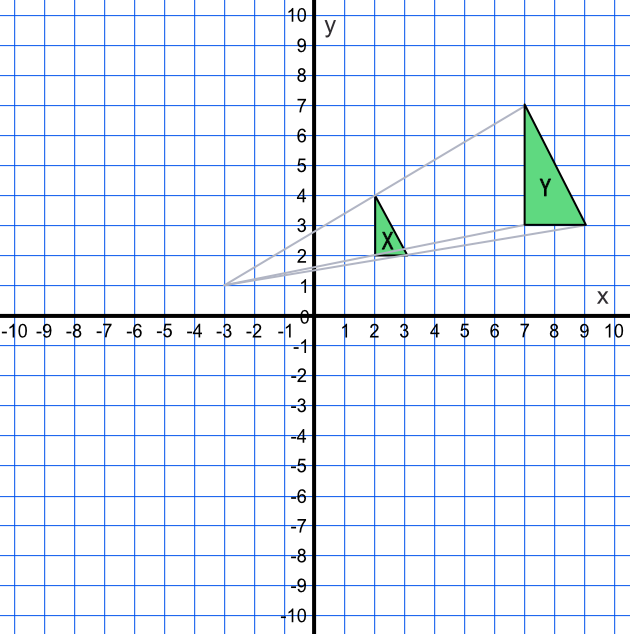
Shape X is mapped onto shape Y. What is the transformation?
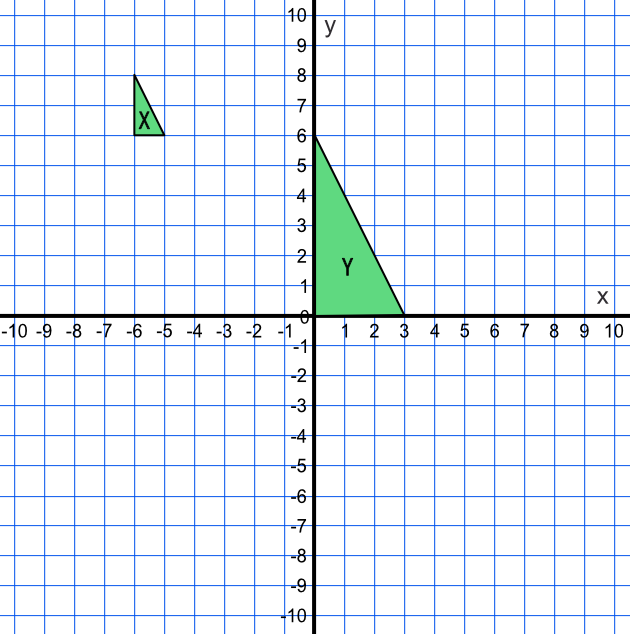
The lengths of the Y shape are three times larger than the lengths of the X shape. THe Scale Factor is 3.
Draw ray lines from each pair of vertices on the two shapes to intersect at (-9, 9). This is the centre of enlargement.
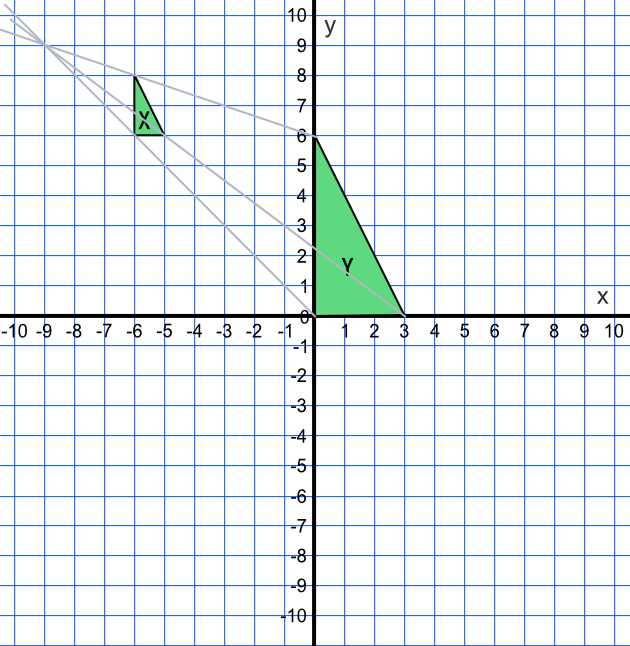
Answer: Enlargement, scale factor 3, centre of enlargement (-9, 9)