Enlargements with a scale factor greater than 1 will always cause the shape to enlarge. If the scale factor is equal to 1, then the enlarged shape will be the same size in the same place. If the scale factor is zero, then the shape will effectively disappear.
If the scale factor is greater than zero, and less than 1, then the enlarged shape will be smaller than the original shape, and will be closer to the centre of enlargement.
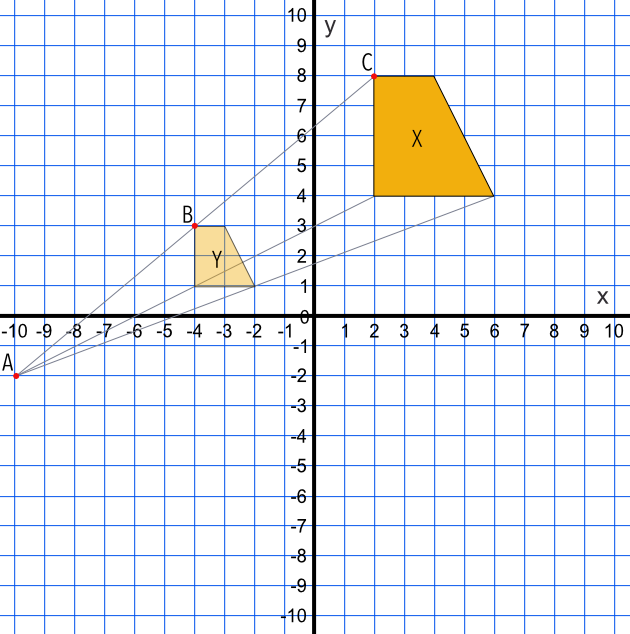
In the diagram below, shape X has been enlarged with a scale factor of 0.5 with a centre of enlargement at (-10, -2) and mapped onto shape Y. The linear dimensions of the shape (the edges) will be half the size of the original. The distance AB will be half the value of the distance AC.
A shape X is enlarged with a scale factor of `frac(1)(2)` with a centre of enlargement (-10, -3). Draw the enlarged shape on the graph.
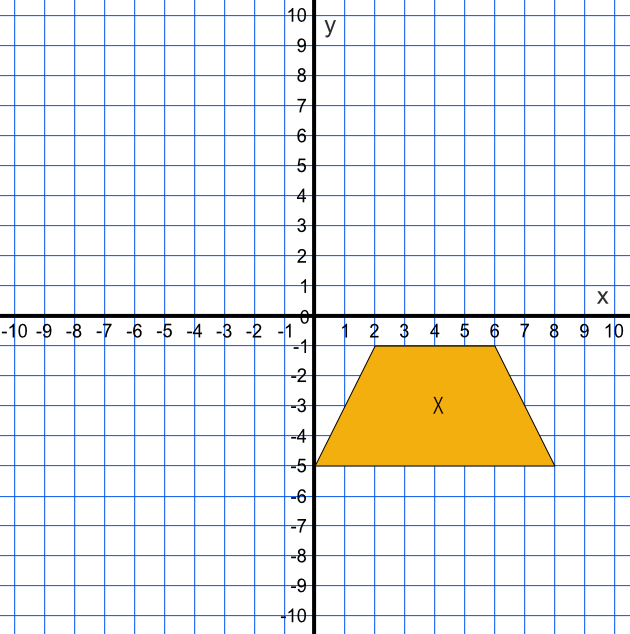
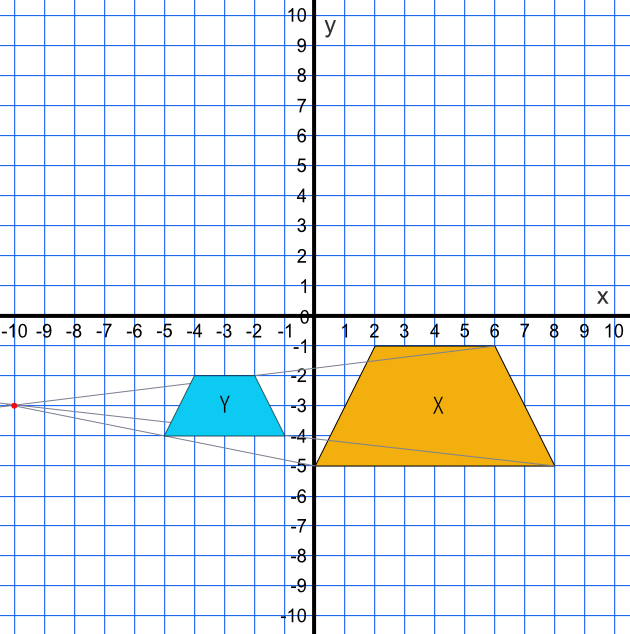
Use ray lines between the vertices of the shape and the centre of enlargement.
Using the grid, determine the half-way points along each ray line: work out the half-way point for the ray line connecting (-10, -3) and the vertex (2, -1). The halfway point is (-4, -2) for that vertex. Repeat for the other vertices.
Check by ensuring that the lengths of the enlarged shape are half the length of the original shape.
Answer:
Shape X has been mapped onto shape Y. Describe fully the transformation that maps shape X onto shape Y.

Draw ray lines from shape X through Shape Y at each vertex. The ray lines will cross at (-7, 8). The size of the enlarged shape is `frac(1)(3)` the size of the original shape; a scale factor of `frac(1)(3)`.
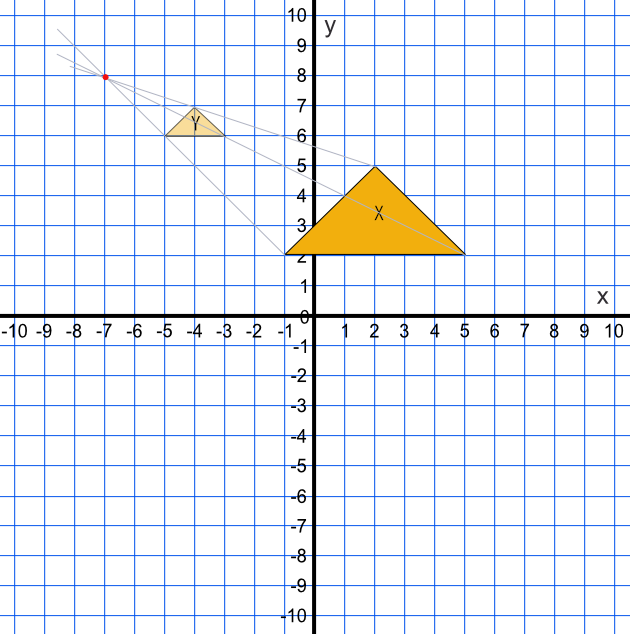
Answer: Enlargement, centre of enlargement (-7, 8), scale factor `frac(1)(3)`